##// END OF EJS Templates
HG_REPOSITORIES » LPP » INSTRUMENTATION » kicadtools
RSS
Improved Polygon rendering by splittig them into lower complexity polygons.
jeandet -
r15:4df93d51b13e default
parent child
Show More
Show file before | Show file after | Hide comments
@@ -0,0 +1,81
1 ####PolyPartition
2
3 PolyPartition is a lightweight C++ library for polygon partition and triangulation. PolyPartition implements multiple algorithms for both convex partitioning and triangulation. Different algorithms produce different quality of results (and their complexity varies accordingly). The implemented methods/algorithms with their advantages and disadvantages are outlined below.
4
5 For input parameters and return values see method declarations in `polypartition.h`. All methods require that the input polygons are not self-intersecting, and are defined in the correct vertex order (conter-clockwise for non-holes, clockwise for holes). Polygon vertices can easily be ordered correctly by calling `TPPLPoly::SetOrientation` method.
6
7 ####Triangulation by ear clipping
8
9 Method: `TPPLPartition::Triangulate_EC`
10
11 Time/Space complexity: `O(n^2)/O(n)`
12
13 Supports holes: Yes, by calling `TPPLPartition::RemoveHoles`
14
15 Quality of solution: Satisfactory in most cases
16
17 Example:
18
19 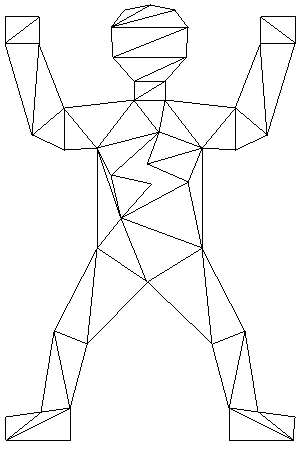![http://polypartition.googlecode.com/svn/trunk/images/tri_ec.png](https://raw.githubusercontent.com/ivanfratric/polypartition/master/images/tri_ec.png)
20
21
22 ####Optimal triangulation in terms of edge length using dynamic programming algorithm
23
24 Method: `TPPLPartition::Triangulate_OPT`
25
26 Time/Space complexity: `O(n^3)/O(n^2)`
27
28 Supports holes: No. You could call `TPPLPartition::RemoveHoles` prior to calling `TPPLPartition::Triangulate_OPT`, but the solution would no longer be optimal, thus defeating the purpose
29
30 Quality of solution: Optimal in terms of minimal edge length
31
32 Example:
33
34 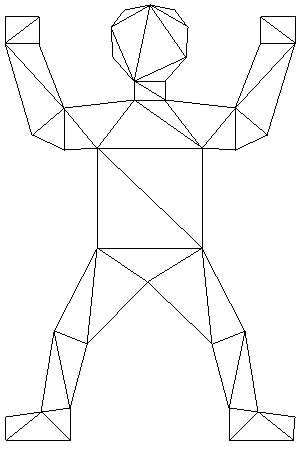![https://raw.githubusercontent.com/ivanfratric/polypartition/master/images/tri_opt.png](https://raw.githubusercontent.com/ivanfratric/polypartition/master/images/tri_opt.png)
35
36
37 ####Triangulation by partition into monotone polygons
38
39 Method: `TPPLPartition::Triangulate_MONO`
40
41 Time/Space complexity: `O(n*log(n))/O(n)`
42
43 Supports holes: Yes, by design
44
45 Quality of solution: Poor. Many thin triangles are created in most cases
46
47 Example:
48
49 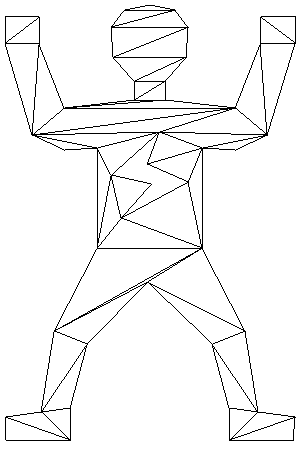![https://raw.githubusercontent.com/ivanfratric/polypartition/master/images/tri_mono.png](https://raw.githubusercontent.com/ivanfratric/polypartition/master/images/tri_mono.png)
50
51
52 ####Convex partition using Hertel-Mehlhorn algorithm
53
54 Method: `TPPLPartition::ConvexPartition_HM`
55
56 Time/Space complexity: `O(n^2)/O(n)`
57
58 Supports holes: Yes, by calling `TPPLPartition::RemoveHoles`
59
60 Quality of solution: At most four times the minimum number of convex polygons is created. However, in practice it works much better than that and often gives optimal partition.
61
62 Example:
63
64 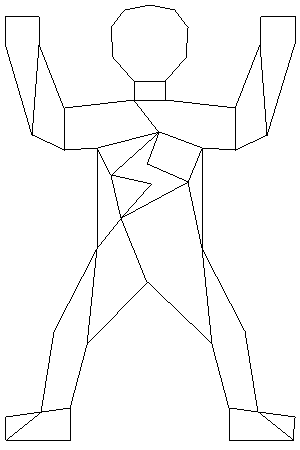![https://raw.githubusercontent.com/ivanfratric/polypartition/master/images/conv_hm.png](https://raw.githubusercontent.com/ivanfratric/polypartition/master/images/conv_hm.png)
65
66
67 ####Optimal convex partition using dynamic programming algorithm by Keil and Snoeyink
68
69 Method: `TPPLPartition::ConvexPartition_OPT`
70
71 Time/Space complexity: `O(n^3)/O(n^3)`
72
73 Supports holes: No. You could call `TPPLPartition::RemoveHoles` prior to calling `TPPLPartition::Triangulate_OPT`, but the solution would no longer be optimal, thus defeating the purpose
74
75 Quality of solution: Optimal. A minimum number of convex polygons is produced
76
77 Example:
78
79 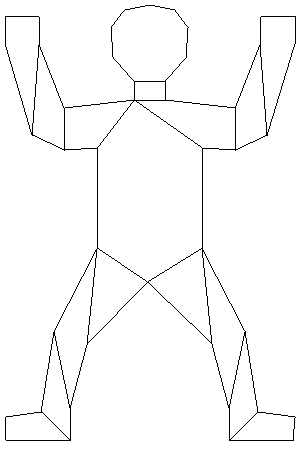![https://raw.githubusercontent.com/ivanfratric/polypartition/master/images/conv_opt.png](https://raw.githubusercontent.com/ivanfratric/polypartition/master/images/conv_opt.png)
80
81
Show file before | Show file after | Hide comments
1 NO CONTENT: new file 100644, binary diff hidden
Show file before | Show file after | Hide comments
1 NO CONTENT: new file 100644, binary diff hidden
Show file before | Show file after | Hide comments
1 NO CONTENT: new file 100644, binary diff hidden
Show file before | Show file after | Hide comments
1 NO CONTENT: new file 100644, binary diff hidden
Show file before | Show file after | Hide comments
1 NO CONTENT: new file 100644, binary diff hidden
Show file before | Show file after | Hide comments
This diff has been collapsed as it changes many lines, (1547 lines changed) Show them Hide them
@@ -0,0 +1,1547
1 //Copyright (C) 2011 by Ivan Fratric
2 //
3 //Permission is hereby granted, free of charge, to any person obtaining a copy
4 //of this software and associated documentation files (the "Software"), to deal
5 //in the Software without restriction, including without limitation the rights
6 //to use, copy, modify, merge, publish, distribute, sublicense, and/or sell
7 //copies of the Software, and to permit persons to whom the Software is
8 //furnished to do so, subject to the following conditions:
9 //
10 //The above copyright notice and this permission notice shall be included in
11 //all copies or substantial portions of the Software.
12 //
13 //THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
14 //IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
15 //FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
16 //AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
17 //LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
18 //OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN
19 //THE SOFTWARE.
20
21
22 #include <stdio.h>
23 #include <string.h>
24 #include <math.h>
25 #include <list>
26 #include <algorithm>
27 #include <set>
28
29 using namespace std;
30
31 #include "polypartition.h"
32
33 #define TPPL_VERTEXTYPE_REGULAR 0
34 #define TPPL_VERTEXTYPE_START 1
35 #define TPPL_VERTEXTYPE_END 2
36 #define TPPL_VERTEXTYPE_SPLIT 3
37 #define TPPL_VERTEXTYPE_MERGE 4
38
39 TPPLPoly::TPPLPoly() {
40 hole = false;
41 numpoints = 0;
42 points = NULL;
43 }
44
45 TPPLPoly::~TPPLPoly() {
46 if(points) delete [] points;
47 }
48
49 void TPPLPoly::Clear() {
50 if(points) delete [] points;
51 hole = false;
52 numpoints = 0;
53 points = NULL;
54 }
55
56 void TPPLPoly::Init(long numpoints) {
57 Clear();
58 this->numpoints = numpoints;
59 points = new TPPLPoint[numpoints];
60 }
61
62 void TPPLPoly::Triangle(TPPLPoint &p1, TPPLPoint &p2, TPPLPoint &p3) {
63 Init(3);
64 points[0] = p1;
65 points[1] = p2;
66 points[2] = p3;
67 }
68
69 TPPLPoly::TPPLPoly(const TPPLPoly &src) {
70 hole = src.hole;
71 numpoints = src.numpoints;
72 points = new TPPLPoint[numpoints];
73 memcpy(points, src.points, numpoints*sizeof(TPPLPoint));
74 }
75
76 TPPLPoly& TPPLPoly::operator=(const TPPLPoly &src) {
77 Clear();
78 hole = src.hole;
79 numpoints = src.numpoints;
80 points = new TPPLPoint[numpoints];
81 memcpy(points, src.points, numpoints*sizeof(TPPLPoint));
82 return *this;
83 }
84
85 int TPPLPoly::GetOrientation() {
86 long i1,i2;
87 tppl_float area = 0;
88 for(i1=0; i1<numpoints; i1++) {
89 i2 = i1+1;
90 if(i2 == numpoints) i2 = 0;
91 area += points[i1].x * points[i2].y - points[i1].y * points[i2].x;
92 }
93 if(area>0) return TPPL_CCW;
94 if(area<0) return TPPL_CW;
95 return 0;
96 }
97
98 void TPPLPoly::SetOrientation(int orientation) {
99 int polyorientation = GetOrientation();
100 if(polyorientation&&(polyorientation!=orientation)) {
101 Invert();
102 }
103 }
104
105 void TPPLPoly::Invert() {
106 long i;
107 TPPLPoint *invpoints;
108
109 invpoints = new TPPLPoint[numpoints];
110 for(i=0;i<numpoints;i++) {
111 invpoints[i] = points[numpoints-i-1];
112 }
113
114 delete [] points;
115 points = invpoints;
116 }
117
118 TPPLPoint TPPLPartition::Normalize(const TPPLPoint &p) {
119 TPPLPoint r;
120 tppl_float n = sqrt(p.x*p.x + p.y*p.y);
121 if(n!=0) {
122 r = p/n;
123 } else {
124 r.x = 0;
125 r.y = 0;
126 }
127 return r;
128 }
129
130 tppl_float TPPLPartition::Distance(const TPPLPoint &p1, const TPPLPoint &p2) {
131 tppl_float dx,dy;
132 dx = p2.x - p1.x;
133 dy = p2.y - p1.y;
134 return(sqrt(dx*dx + dy*dy));
135 }
136
137 //checks if two lines intersect
138 int TPPLPartition::Intersects(TPPLPoint &p11, TPPLPoint &p12, TPPLPoint &p21, TPPLPoint &p22) {
139 if((p11.x == p21.x)&&(p11.y == p21.y)) return 0;
140 if((p11.x == p22.x)&&(p11.y == p22.y)) return 0;
141 if((p12.x == p21.x)&&(p12.y == p21.y)) return 0;
142 if((p12.x == p22.x)&&(p12.y == p22.y)) return 0;
143
144 TPPLPoint v1ort,v2ort,v;
145 tppl_float dot11,dot12,dot21,dot22;
146
147 v1ort.x = p12.y-p11.y;
148 v1ort.y = p11.x-p12.x;
149
150 v2ort.x = p22.y-p21.y;
151 v2ort.y = p21.x-p22.x;
152
153 v = p21-p11;
154 dot21 = v.x*v1ort.x + v.y*v1ort.y;
155 v = p22-p11;
156 dot22 = v.x*v1ort.x + v.y*v1ort.y;
157
158 v = p11-p21;
159 dot11 = v.x*v2ort.x + v.y*v2ort.y;
160 v = p12-p21;
161 dot12 = v.x*v2ort.x + v.y*v2ort.y;
162
163 if(dot11*dot12>0) return 0;
164 if(dot21*dot22>0) return 0;
165
166 return 1;
167 }
168
169 //removes holes from inpolys by merging them with non-holes
170 int TPPLPartition::RemoveHoles(list<TPPLPoly> *inpolys, list<TPPLPoly> *outpolys) {
171 list<TPPLPoly> polys;
172 list<TPPLPoly>::iterator holeiter,polyiter,iter,iter2;
173 long i,i2,holepointindex,polypointindex;
174 TPPLPoint holepoint,polypoint,bestpolypoint;
175 TPPLPoint linep1,linep2;
176 TPPLPoint v1,v2;
177 TPPLPoly newpoly;
178 bool hasholes;
179 bool pointvisible;
180 bool pointfound;
181
182 //check for trivial case (no holes)
183 hasholes = false;
184 for(iter = inpolys->begin(); iter!=inpolys->end(); iter++) {
185 if(iter->IsHole()) {
186 hasholes = true;
187 break;
188 }
189 }
190 if(!hasholes) {
191 for(iter = inpolys->begin(); iter!=inpolys->end(); iter++) {
192 outpolys->push_back(*iter);
193 }
194 return 1;
195 }
196
197 polys = *inpolys;
198
199 while(1) {
200 //find the hole point with the largest x
201 hasholes = false;
202 for(iter = polys.begin(); iter!=polys.end(); iter++) {
203 if(!iter->IsHole()) continue;
204
205 if(!hasholes) {
206 hasholes = true;
207 holeiter = iter;
208 holepointindex = 0;
209 }
210
211 for(i=0; i < iter->GetNumPoints(); i++) {
212 if(iter->GetPoint(i).x > holeiter->GetPoint(holepointindex).x) {
213 holeiter = iter;
214 holepointindex = i;
215 }
216 }
217 }
218 if(!hasholes) break;
219 holepoint = holeiter->GetPoint(holepointindex);
220
221 pointfound = false;
222 for(iter = polys.begin(); iter!=polys.end(); iter++) {
223 if(iter->IsHole()) continue;
224 for(i=0; i < iter->GetNumPoints(); i++) {
225 if(iter->GetPoint(i).x <= holepoint.x) continue;
226 if(!InCone(iter->GetPoint((i+iter->GetNumPoints()-1)%(iter->GetNumPoints())),
227 iter->GetPoint(i),
228 iter->GetPoint((i+1)%(iter->GetNumPoints())),
229 holepoint))
230 continue;
231 polypoint = iter->GetPoint(i);
232 if(pointfound) {
233 v1 = Normalize(polypoint-holepoint);
234 v2 = Normalize(bestpolypoint-holepoint);
235 if(v2.x > v1.x) continue;
236 }
237 pointvisible = true;
238 for(iter2 = polys.begin(); iter2!=polys.end(); iter2++) {
239 if(iter2->IsHole()) continue;
240 for(i2=0; i2 < iter2->GetNumPoints(); i2++) {
241 linep1 = iter2->GetPoint(i2);
242 linep2 = iter2->GetPoint((i2+1)%(iter2->GetNumPoints()));
243 if(Intersects(holepoint,polypoint,linep1,linep2)) {
244 pointvisible = false;
245 break;
246 }
247 }
248 if(!pointvisible) break;
249 }
250 if(pointvisible) {
251 pointfound = true;
252 bestpolypoint = polypoint;
253 polyiter = iter;
254 polypointindex = i;
255 }
256 }
257 }
258
259 if(!pointfound) return 0;
260
261 newpoly.Init(holeiter->GetNumPoints() + polyiter->GetNumPoints() + 2);
262 i2 = 0;
263 for(i=0;i<=polypointindex;i++) {
264 newpoly[i2] = polyiter->GetPoint(i);
265 i2++;
266 }
267 for(i=0;i<=holeiter->GetNumPoints();i++) {
268 newpoly[i2] = holeiter->GetPoint((i+holepointindex)%holeiter->GetNumPoints());
269 i2++;
270 }
271 for(i=polypointindex;i<polyiter->GetNumPoints();i++) {
272 newpoly[i2] = polyiter->GetPoint(i);
273 i2++;
274 }
275
276 polys.erase(holeiter);
277 polys.erase(polyiter);
278 polys.push_back(newpoly);
279 }
280
281 for(iter = polys.begin(); iter!=polys.end(); iter++) {
282 outpolys->push_back(*iter);
283 }
284
285 return 1;
286 }
287
288 bool TPPLPartition::IsConvex(TPPLPoint& p1, TPPLPoint& p2, TPPLPoint& p3) {
289 tppl_float tmp;
290 tmp = (p3.y-p1.y)*(p2.x-p1.x)-(p3.x-p1.x)*(p2.y-p1.y);
291 if(tmp>0) return 1;
292 else return 0;
293 }
294
295 bool TPPLPartition::IsReflex(TPPLPoint& p1, TPPLPoint& p2, TPPLPoint& p3) {
296 tppl_float tmp;
297 tmp = (p3.y-p1.y)*(p2.x-p1.x)-(p3.x-p1.x)*(p2.y-p1.y);
298 if(tmp<0) return 1;
299 else return 0;
300 }
301
302 bool TPPLPartition::IsInside(TPPLPoint& p1, TPPLPoint& p2, TPPLPoint& p3, TPPLPoint &p) {
303 if(IsConvex(p1,p,p2)) return false;
304 if(IsConvex(p2,p,p3)) return false;
305 if(IsConvex(p3,p,p1)) return false;
306 return true;
307 }
308
309 bool TPPLPartition::InCone(TPPLPoint &p1, TPPLPoint &p2, TPPLPoint &p3, TPPLPoint &p) {
310 bool convex;
311
312 convex = IsConvex(p1,p2,p3);
313
314 if(convex) {
315 if(!IsConvex(p1,p2,p)) return false;
316 if(!IsConvex(p2,p3,p)) return false;
317 return true;
318 } else {
319 if(IsConvex(p1,p2,p)) return true;
320 if(IsConvex(p2,p3,p)) return true;
321 return false;
322 }
323 }
324
325 bool TPPLPartition::InCone(PartitionVertex *v, TPPLPoint &p) {
326 TPPLPoint p1,p2,p3;
327
328 p1 = v->previous->p;
329 p2 = v->p;
330 p3 = v->next->p;
331
332 return InCone(p1,p2,p3,p);
333 }
334
335 void TPPLPartition::UpdateVertexReflexity(PartitionVertex *v) {
336 PartitionVertex *v1,*v3;
337 v1 = v->previous;
338 v3 = v->next;
339 v->isConvex = !IsReflex(v1->p,v->p,v3->p);
340 }
341
342 void TPPLPartition::UpdateVertex(PartitionVertex *v, PartitionVertex *vertices, long numvertices) {
343 long i;
344 PartitionVertex *v1,*v3;
345 TPPLPoint vec1,vec3;
346
347 v1 = v->previous;
348 v3 = v->next;
349
350 v->isConvex = IsConvex(v1->p,v->p,v3->p);
351
352 vec1 = Normalize(v1->p - v->p);
353 vec3 = Normalize(v3->p - v->p);
354 v->angle = vec1.x*vec3.x + vec1.y*vec3.y;
355
356 if(v->isConvex) {
357 v->isEar = true;
358 for(i=0;i<numvertices;i++) {
359 if((vertices[i].p.x==v->p.x)&&(vertices[i].p.y==v->p.y)) continue;
360 if((vertices[i].p.x==v1->p.x)&&(vertices[i].p.y==v1->p.y)) continue;
361 if((vertices[i].p.x==v3->p.x)&&(vertices[i].p.y==v3->p.y)) continue;
362 if(IsInside(v1->p,v->p,v3->p,vertices[i].p)) {
363 v->isEar = false;
364 break;
365 }
366 }
367 } else {
368 v->isEar = false;
369 }
370 }
371
372 //triangulation by ear removal
373 int TPPLPartition::Triangulate_EC(TPPLPoly *poly, list<TPPLPoly> *triangles) {
374 long numvertices;
375 PartitionVertex *vertices;
376 PartitionVertex *ear;
377 TPPLPoly triangle;
378 long i,j;
379 bool earfound;
380
381 if(poly->GetNumPoints() < 3) return 0;
382 if(poly->GetNumPoints() == 3) {
383 triangles->push_back(*poly);
384 return 1;
385 }
386
387 numvertices = poly->GetNumPoints();
388
389 vertices = new PartitionVertex[numvertices];
390 for(i=0;i<numvertices;i++) {
391 vertices[i].isActive = true;
392 vertices[i].p = poly->GetPoint(i);
393 if(i==(numvertices-1)) vertices[i].next=&(vertices[0]);
394 else vertices[i].next=&(vertices[i+1]);
395 if(i==0) vertices[i].previous = &(vertices[numvertices-1]);
396 else vertices[i].previous = &(vertices[i-1]);
397 }
398 for(i=0;i<numvertices;i++) {
399 UpdateVertex(&vertices[i],vertices,numvertices);
400 }
401
402 for(i=0;i<numvertices-3;i++) {
403 earfound = false;
404 //find the most extruded ear
405 for(j=0;j<numvertices;j++) {
406 if(!vertices[j].isActive) continue;
407 if(!vertices[j].isEar) continue;
408 if(!earfound) {
409 earfound = true;
410 ear = &(vertices[j]);
411 } else {
412 if(vertices[j].angle > ear->angle) {
413 ear = &(vertices[j]);
414 }
415 }
416 }
417 if(!earfound) {
418 delete [] vertices;
419 return 0;
420 }
421
422 triangle.Triangle(ear->previous->p,ear->p,ear->next->p);
423 triangles->push_back(triangle);
424
425 ear->isActive = false;
426 ear->previous->next = ear->next;
427 ear->next->previous = ear->previous;
428
429 if(i==numvertices-4) break;
430
431 UpdateVertex(ear->previous,vertices,numvertices);
432 UpdateVertex(ear->next,vertices,numvertices);
433 }
434 for(i=0;i<numvertices;i++) {
435 if(vertices[i].isActive) {
436 triangle.Triangle(vertices[i].previous->p,vertices[i].p,vertices[i].next->p);
437 triangles->push_back(triangle);
438 break;
439 }
440 }
441
442 delete [] vertices;
443
444 return 1;
445 }
446
447 int TPPLPartition::Triangulate_EC(list<TPPLPoly> *inpolys, list<TPPLPoly> *triangles) {
448 list<TPPLPoly> outpolys;
449 list<TPPLPoly>::iterator iter;
450
451 if(!RemoveHoles(inpolys,&outpolys)) return 0;
452 for(iter=outpolys.begin();iter!=outpolys.end();iter++) {
453 if(!Triangulate_EC(&(*iter),triangles)) return 0;
454 }
455 return 1;
456 }
457
458 int TPPLPartition::ConvexPartition_HM(TPPLPoly *poly, list<TPPLPoly> *parts) {
459 list<TPPLPoly> triangles;
460 list<TPPLPoly>::iterator iter1,iter2;
461 TPPLPoly *poly1,*poly2;
462 TPPLPoly newpoly;
463 TPPLPoint d1,d2,p1,p2,p3;
464 long i11,i12,i21,i22,i13,i23,j,k;
465 bool isdiagonal;
466 long numreflex;
467
468 //check if the poly is already convex
469 numreflex = 0;
470 for(i11=0;i11<poly->GetNumPoints();i11++) {
471 if(i11==0) i12 = poly->GetNumPoints()-1;
472 else i12=i11-1;
473 if(i11==(poly->GetNumPoints()-1)) i13=0;
474 else i13=i11+1;
475 if(IsReflex(poly->GetPoint(i12),poly->GetPoint(i11),poly->GetPoint(i13))) {
476 numreflex = 1;
477 break;
478 }
479 }
480 if(numreflex == 0) {
481 parts->push_back(*poly);
482 return 1;
483 }
484
485 if(!Triangulate_EC(poly,&triangles)) return 0;
486
487 for(iter1 = triangles.begin(); iter1 != triangles.end(); iter1++) {
488 poly1 = &(*iter1);
489 for(i11=0;i11<poly1->GetNumPoints();i11++) {
490 d1 = poly1->GetPoint(i11);
491 i12 = (i11+1)%(poly1->GetNumPoints());
492 d2 = poly1->GetPoint(i12);
493
494 isdiagonal = false;
495 for(iter2 = iter1; iter2 != triangles.end(); iter2++) {
496 if(iter1 == iter2) continue;
497 poly2 = &(*iter2);
498
499 for(i21=0;i21<poly2->GetNumPoints();i21++) {
500 if((d2.x != poly2->GetPoint(i21).x)||(d2.y != poly2->GetPoint(i21).y)) continue;
501 i22 = (i21+1)%(poly2->GetNumPoints());
502 if((d1.x != poly2->GetPoint(i22).x)||(d1.y != poly2->GetPoint(i22).y)) continue;
503 isdiagonal = true;
504 break;
505 }
506 if(isdiagonal) break;
507 }
508
509 if(!isdiagonal) continue;
510
511 p2 = poly1->GetPoint(i11);
512 if(i11 == 0) i13 = poly1->GetNumPoints()-1;
513 else i13 = i11-1;
514 p1 = poly1->GetPoint(i13);
515 if(i22 == (poly2->GetNumPoints()-1)) i23 = 0;
516 else i23 = i22+1;
517 p3 = poly2->GetPoint(i23);
518
519 if(!IsConvex(p1,p2,p3)) continue;
520
521 p2 = poly1->GetPoint(i12);
522 if(i12 == (poly1->GetNumPoints()-1)) i13 = 0;
523 else i13 = i12+1;
524 p3 = poly1->GetPoint(i13);
525 if(i21 == 0) i23 = poly2->GetNumPoints()-1;
526 else i23 = i21-1;
527 p1 = poly2->GetPoint(i23);
528
529 if(!IsConvex(p1,p2,p3)) continue;
530
531 newpoly.Init(poly1->GetNumPoints()+poly2->GetNumPoints()-2);
532 k = 0;
533 for(j=i12;j!=i11;j=(j+1)%(poly1->GetNumPoints())) {
534 newpoly[k] = poly1->GetPoint(j);
535 k++;
536 }
537 for(j=i22;j!=i21;j=(j+1)%(poly2->GetNumPoints())) {
538 newpoly[k] = poly2->GetPoint(j);
539 k++;
540 }
541
542 triangles.erase(iter2);
543 *iter1 = newpoly;
544 poly1 = &(*iter1);
545 i11 = -1;
546
547 continue;
548 }
549 }
550
551 for(iter1 = triangles.begin(); iter1 != triangles.end(); iter1++) {
552 parts->push_back(*iter1);
553 }
554
555 return 1;
556 }
557
558 int TPPLPartition::ConvexPartition_HM(list<TPPLPoly> *inpolys, list<TPPLPoly> *parts) {
559 list<TPPLPoly> outpolys;
560 list<TPPLPoly>::iterator iter;
561
562 if(!RemoveHoles(inpolys,&outpolys)) return 0;
563 for(iter=outpolys.begin();iter!=outpolys.end();iter++) {
564 if(!ConvexPartition_HM(&(*iter),parts)) return 0;
565 }
566 return 1;
567 }
568
569 //minimum-weight polygon triangulation by dynamic programming
570 //O(n^3) time complexity
571 //O(n^2) space complexity
572 int TPPLPartition::Triangulate_OPT(TPPLPoly *poly, list<TPPLPoly> *triangles) {
573 long i,j,k,gap,n;
574 DPState **dpstates;
575 TPPLPoint p1,p2,p3,p4;
576 long bestvertex;
577 tppl_float weight,minweight,d1,d2;
578 Diagonal diagonal,newdiagonal;
579 list<Diagonal> diagonals;
580 TPPLPoly triangle;
581 int ret = 1;
582
583 n = poly->GetNumPoints();
584 dpstates = new DPState *[n];
585 for(i=1;i<n;i++) {
586 dpstates[i] = new DPState[i];
587 }
588
589 //init states and visibility
590 for(i=0;i<(n-1);i++) {
591 p1 = poly->GetPoint(i);
592 for(j=i+1;j<n;j++) {
593 dpstates[j][i].visible = true;
594 dpstates[j][i].weight = 0;
595 dpstates[j][i].bestvertex = -1;
596 if(j!=(i+1)) {
597 p2 = poly->GetPoint(j);
598
599 //visibility check
600 if(i==0) p3 = poly->GetPoint(n-1);
601 else p3 = poly->GetPoint(i-1);
602 if(i==(n-1)) p4 = poly->GetPoint(0);
603 else p4 = poly->GetPoint(i+1);
604 if(!InCone(p3,p1,p4,p2)) {
605 dpstates[j][i].visible = false;
606 continue;
607 }
608
609 if(j==0) p3 = poly->GetPoint(n-1);
610 else p3 = poly->GetPoint(j-1);
611 if(j==(n-1)) p4 = poly->GetPoint(0);
612 else p4 = poly->GetPoint(j+1);
613 if(!InCone(p3,p2,p4,p1)) {
614 dpstates[j][i].visible = false;
615 continue;
616 }
617
618 for(k=0;k<n;k++) {
619 p3 = poly->GetPoint(k);
620 if(k==(n-1)) p4 = poly->GetPoint(0);
621 else p4 = poly->GetPoint(k+1);
622 if(Intersects(p1,p2,p3,p4)) {
623 dpstates[j][i].visible = false;
624 break;
625 }
626 }
627 }
628 }
629 }
630 dpstates[n-1][0].visible = true;
631 dpstates[n-1][0].weight = 0;
632 dpstates[n-1][0].bestvertex = -1;
633
634 for(gap = 2; gap<n; gap++) {
635 for(i=0; i<(n-gap); i++) {
636 j = i+gap;
637 if(!dpstates[j][i].visible) continue;
638 bestvertex = -1;
639 for(k=(i+1);k<j;k++) {
640 if(!dpstates[k][i].visible) continue;
641 if(!dpstates[j][k].visible) continue;
642
643 if(k<=(i+1)) d1=0;
644 else d1 = Distance(poly->GetPoint(i),poly->GetPoint(k));
645 if(j<=(k+1)) d2=0;
646 else d2 = Distance(poly->GetPoint(k),poly->GetPoint(j));
647
648 weight = dpstates[k][i].weight + dpstates[j][k].weight + d1 + d2;
649
650 if((bestvertex == -1)||(weight<minweight)) {
651 bestvertex = k;
652 minweight = weight;
653 }
654 }
655 if(bestvertex == -1) {
656 for(i=1;i<n;i++) {
657 delete [] dpstates[i];
658 }
659 delete [] dpstates;
660
661 return 0;
662 }
663
664 dpstates[j][i].bestvertex = bestvertex;
665 dpstates[j][i].weight = minweight;
666 }
667 }
668
669 newdiagonal.index1 = 0;
670 newdiagonal.index2 = n-1;
671 diagonals.push_back(newdiagonal);
672 while(!diagonals.empty()) {
673 diagonal = *(diagonals.begin());
674 diagonals.pop_front();
675 bestvertex = dpstates[diagonal.index2][diagonal.index1].bestvertex;
676 if(bestvertex == -1) {
677 ret = 0;
678 break;
679 }
680 triangle.Triangle(poly->GetPoint(diagonal.index1),poly->GetPoint(bestvertex),poly->GetPoint(diagonal.index2));
681 triangles->push_back(triangle);
682 if(bestvertex > (diagonal.index1+1)) {
683 newdiagonal.index1 = diagonal.index1;
684 newdiagonal.index2 = bestvertex;
685 diagonals.push_back(newdiagonal);
686 }
687 if(diagonal.index2 > (bestvertex+1)) {
688 newdiagonal.index1 = bestvertex;
689 newdiagonal.index2 = diagonal.index2;
690 diagonals.push_back(newdiagonal);
691 }
692 }
693
694 for(i=1;i<n;i++) {
695 delete [] dpstates[i];
696 }
697 delete [] dpstates;
698
699 return ret;
700 }
701
702 void TPPLPartition::UpdateState(long a, long b, long w, long i, long j, DPState2 **dpstates) {
703 Diagonal newdiagonal;
704 list<Diagonal> *pairs;
705 long w2;
706
707 w2 = dpstates[a][b].weight;
708 if(w>w2) return;
709
710 pairs = &(dpstates[a][b].pairs);
711 newdiagonal.index1 = i;
712 newdiagonal.index2 = j;
713
714 if(w<w2) {
715 pairs->clear();
716 pairs->push_front(newdiagonal);
717 dpstates[a][b].weight = w;
718 } else {
719 if((!pairs->empty())&&(i <= pairs->begin()->index1)) return;
720 while((!pairs->empty())&&(pairs->begin()->index2 >= j)) pairs->pop_front();
721 pairs->push_front(newdiagonal);
722 }
723 }
724
725 void TPPLPartition::TypeA(long i, long j, long k, PartitionVertex *vertices, DPState2 **dpstates) {
726 list<Diagonal> *pairs;
727 list<Diagonal>::iterator iter,lastiter;
728 long top;
729 long w;
730
731 if(!dpstates[i][j].visible) return;
732 top = j;
733 w = dpstates[i][j].weight;
734 if(k-j > 1) {
735 if (!dpstates[j][k].visible) return;
736 w += dpstates[j][k].weight + 1;
737 }
738 if(j-i > 1) {
739 pairs = &(dpstates[i][j].pairs);
740 iter = pairs->end();
741 lastiter = pairs->end();
742 while(iter!=pairs->begin()) {
743 iter--;
744 if(!IsReflex(vertices[iter->index2].p,vertices[j].p,vertices[k].p)) lastiter = iter;
745 else break;
746 }
747 if(lastiter == pairs->end()) w++;
748 else {
749 if(IsReflex(vertices[k].p,vertices[i].p,vertices[lastiter->index1].p)) w++;
750 else top = lastiter->index1;
751 }
752 }
753 UpdateState(i,k,w,top,j,dpstates);
754 }
755
756 void TPPLPartition::TypeB(long i, long j, long k, PartitionVertex *vertices, DPState2 **dpstates) {
757 list<Diagonal> *pairs;
758 list<Diagonal>::iterator iter,lastiter;
759 long top;
760 long w;
761
762 if(!dpstates[j][k].visible) return;
763 top = j;
764 w = dpstates[j][k].weight;
765
766 if (j-i > 1) {
767 if (!dpstates[i][j].visible) return;
768 w += dpstates[i][j].weight + 1;
769 }
770 if (k-j > 1) {
771 pairs = &(dpstates[j][k].pairs);
772
773 iter = pairs->begin();
774 if((!pairs->empty())&&(!IsReflex(vertices[i].p,vertices[j].p,vertices[iter->index1].p))) {
775 lastiter = iter;
776 while(iter!=pairs->end()) {
777 if(!IsReflex(vertices[i].p,vertices[j].p,vertices[iter->index1].p)) {
778 lastiter = iter;
779 iter++;
780 }
781 else break;
782 }
783 if(IsReflex(vertices[lastiter->index2].p,vertices[k].p,vertices[i].p)) w++;
784 else top = lastiter->index2;
785 } else w++;
786 }
787 UpdateState(i,k,w,j,top,dpstates);
788 }
789
790 int TPPLPartition::ConvexPartition_OPT(TPPLPoly *poly, list<TPPLPoly> *parts) {
791 TPPLPoint p1,p2,p3,p4;
792 PartitionVertex *vertices;
793 DPState2 **dpstates;
794 long i,j,k,n,gap;
795 list<Diagonal> diagonals,diagonals2;
796 Diagonal diagonal,newdiagonal;
797 list<Diagonal> *pairs,*pairs2;
798 list<Diagonal>::iterator iter,iter2;
799 int ret;
800 TPPLPoly newpoly;
801 list<long> indices;
802 list<long>::iterator iiter;
803 bool ijreal,jkreal;
804
805 n = poly->GetNumPoints();
806 vertices = new PartitionVertex[n];
807
808 dpstates = new DPState2 *[n];
809 for(i=0;i<n;i++) {
810 dpstates[i] = new DPState2[n];
811 }
812
813 //init vertex information
814 for(i=0;i<n;i++) {
815 vertices[i].p = poly->GetPoint(i);
816 vertices[i].isActive = true;
817 if(i==0) vertices[i].previous = &(vertices[n-1]);
818 else vertices[i].previous = &(vertices[i-1]);
819 if(i==(poly->GetNumPoints()-1)) vertices[i].next = &(vertices[0]);
820 else vertices[i].next = &(vertices[i+1]);
821 }
822 for(i=1;i<n;i++) {
823 UpdateVertexReflexity(&(vertices[i]));
824 }
825
826 //init states and visibility
827 for(i=0;i<(n-1);i++) {
828 p1 = poly->GetPoint(i);
829 for(j=i+1;j<n;j++) {
830 dpstates[i][j].visible = true;
831 if(j==i+1) {
832 dpstates[i][j].weight = 0;
833 } else {
834 dpstates[i][j].weight = 2147483647;
835 }
836 if(j!=(i+1)) {
837 p2 = poly->GetPoint(j);
838
839 //visibility check
840 if(!InCone(&vertices[i],p2)) {
841 dpstates[i][j].visible = false;
842 continue;
843 }
844 if(!InCone(&vertices[j],p1)) {
845 dpstates[i][j].visible = false;
846 continue;
847 }
848
849 for(k=0;k<n;k++) {
850 p3 = poly->GetPoint(k);
851 if(k==(n-1)) p4 = poly->GetPoint(0);
852 else p4 = poly->GetPoint(k+1);
853 if(Intersects(p1,p2,p3,p4)) {
854 dpstates[i][j].visible = false;
855 break;
856 }
857 }
858 }
859 }
860 }
861 for(i=0;i<(n-2);i++) {
862 j = i+2;
863 if(dpstates[i][j].visible) {
864 dpstates[i][j].weight = 0;
865 newdiagonal.index1 = i+1;
866 newdiagonal.index2 = i+1;
867 dpstates[i][j].pairs.push_back(newdiagonal);
868 }
869 }
870
871 dpstates[0][n-1].visible = true;
872 vertices[0].isConvex = false; //by convention
873
874 for(gap=3; gap<n; gap++) {
875 for(i=0;i<n-gap;i++) {
876 if(vertices[i].isConvex) continue;
877 k = i+gap;
878 if(dpstates[i][k].visible) {
879 if(!vertices[k].isConvex) {
880 for(j=i+1;j<k;j++) TypeA(i,j,k,vertices,dpstates);
881 } else {
882 for(j=i+1;j<(k-1);j++) {
883 if(vertices[j].isConvex) continue;
884 TypeA(i,j,k,vertices,dpstates);
885 }
886 TypeA(i,k-1,k,vertices,dpstates);
887 }
888 }
889 }
890 for(k=gap;k<n;k++) {
891 if(vertices[k].isConvex) continue;
892 i = k-gap;
893 if((vertices[i].isConvex)&&(dpstates[i][k].visible)) {
894 TypeB(i,i+1,k,vertices,dpstates);
895 for(j=i+2;j<k;j++) {
896 if(vertices[j].isConvex) continue;
897 TypeB(i,j,k,vertices,dpstates);
898 }
899 }
900 }
901 }
902
903
904 //recover solution
905 ret = 1;
906 newdiagonal.index1 = 0;
907 newdiagonal.index2 = n-1;
908 diagonals.push_front(newdiagonal);
909 while(!diagonals.empty()) {
910 diagonal = *(diagonals.begin());
911 diagonals.pop_front();
912 if((diagonal.index2 - diagonal.index1) <=1) continue;
913 pairs = &(dpstates[diagonal.index1][diagonal.index2].pairs);
914 if(pairs->empty()) {
915 ret = 0;
916 break;
917 }
918 if(!vertices[diagonal.index1].isConvex) {
919 iter = pairs->end();
920 iter--;
921 j = iter->index2;
922 newdiagonal.index1 = j;
923 newdiagonal.index2 = diagonal.index2;
924 diagonals.push_front(newdiagonal);
925 if((j - diagonal.index1)>1) {
926 if(iter->index1 != iter->index2) {
927 pairs2 = &(dpstates[diagonal.index1][j].pairs);
928 while(1) {
929 if(pairs2->empty()) {
930 ret = 0;
931 break;
932 }
933 iter2 = pairs2->end();
934 iter2--;
935 if(iter->index1 != iter2->index1) pairs2->pop_back();
936 else break;
937 }
938 if(ret == 0) break;
939 }
940 newdiagonal.index1 = diagonal.index1;
941 newdiagonal.index2 = j;
942 diagonals.push_front(newdiagonal);
943 }
944 } else {
945 iter = pairs->begin();
946 j = iter->index1;
947 newdiagonal.index1 = diagonal.index1;
948 newdiagonal.index2 = j;
949 diagonals.push_front(newdiagonal);
950 if((diagonal.index2 - j) > 1) {
951 if(iter->index1 != iter->index2) {
952 pairs2 = &(dpstates[j][diagonal.index2].pairs);
953 while(1) {
954 if(pairs2->empty()) {
955 ret = 0;
956 break;
957 }
958 iter2 = pairs2->begin();
959 if(iter->index2 != iter2->index2) pairs2->pop_front();
960 else break;
961 }
962 if(ret == 0) break;
963 }
964 newdiagonal.index1 = j;
965 newdiagonal.index2 = diagonal.index2;
966 diagonals.push_front(newdiagonal);
967 }
968 }
969 }
970
971 if(ret == 0) {
972 for(i=0;i<n;i++) {
973 delete [] dpstates[i];
974 }
975 delete [] dpstates;
976 delete [] vertices;
977
978 return ret;
979 }
980
981 newdiagonal.index1 = 0;
982 newdiagonal.index2 = n-1;
983 diagonals.push_front(newdiagonal);
984 while(!diagonals.empty()) {
985 diagonal = *(diagonals.begin());
986 diagonals.pop_front();
987 if((diagonal.index2 - diagonal.index1) <= 1) continue;
988
989 indices.clear();
990 diagonals2.clear();
991 indices.push_back(diagonal.index1);
992 indices.push_back(diagonal.index2);
993 diagonals2.push_front(diagonal);
994
995 while(!diagonals2.empty()) {
996 diagonal = *(diagonals2.begin());
997 diagonals2.pop_front();
998 if((diagonal.index2 - diagonal.index1) <= 1) continue;
999 ijreal = true;
1000 jkreal = true;
1001 pairs = &(dpstates[diagonal.index1][diagonal.index2].pairs);
1002 if(!vertices[diagonal.index1].isConvex) {
1003 iter = pairs->end();
1004 iter--;
1005 j = iter->index2;
1006 if(iter->index1 != iter->index2) ijreal = false;
1007 } else {
1008 iter = pairs->begin();
1009 j = iter->index1;
1010 if(iter->index1 != iter->index2) jkreal = false;
1011 }
1012
1013 newdiagonal.index1 = diagonal.index1;
1014 newdiagonal.index2 = j;
1015 if(ijreal) {
1016 diagonals.push_back(newdiagonal);
1017 } else {
1018 diagonals2.push_back(newdiagonal);
1019 }
1020
1021 newdiagonal.index1 = j;
1022 newdiagonal.index2 = diagonal.index2;
1023 if(jkreal) {
1024 diagonals.push_back(newdiagonal);
1025 } else {
1026 diagonals2.push_back(newdiagonal);
1027 }
1028
1029 indices.push_back(j);
1030 }
1031
1032 indices.sort();
1033 newpoly.Init((long)indices.size());
1034 k=0;
1035 for(iiter = indices.begin();iiter!=indices.end();iiter++) {
1036 newpoly[k] = vertices[*iiter].p;
1037 k++;
1038 }
1039 parts->push_back(newpoly);
1040 }
1041
1042 for(i=0;i<n;i++) {
1043 delete [] dpstates[i];
1044 }
1045 delete [] dpstates;
1046 delete [] vertices;
1047
1048 return ret;
1049 }
1050
1051 //triangulates a set of polygons by first partitioning them into monotone polygons
1052 //O(n*log(n)) time complexity, O(n) space complexity
1053 //the algorithm used here is outlined in the book
1054 //"Computational Geometry: Algorithms and Applications"
1055 //by Mark de Berg, Otfried Cheong, Marc van Kreveld and Mark Overmars
1056 int TPPLPartition::MonotonePartition(list<TPPLPoly> *inpolys, list<TPPLPoly> *monotonePolys) {
1057 list<TPPLPoly>::iterator iter;
1058 MonotoneVertex *vertices;
1059 long i,numvertices,vindex,vindex2,newnumvertices,maxnumvertices;
1060 long polystartindex, polyendindex;
1061 TPPLPoly *poly;
1062 MonotoneVertex *v,*v2,*vprev,*vnext;
1063 ScanLineEdge newedge;
1064 bool error = false;
1065
1066 numvertices = 0;
1067 for(iter = inpolys->begin(); iter != inpolys->end(); iter++) {
1068 numvertices += iter->GetNumPoints();
1069 }
1070
1071 maxnumvertices = numvertices*3;
1072 vertices = new MonotoneVertex[maxnumvertices];
1073 newnumvertices = numvertices;
1074
1075 polystartindex = 0;
1076 for(iter = inpolys->begin(); iter != inpolys->end(); iter++) {
1077 poly = &(*iter);
1078 polyendindex = polystartindex + poly->GetNumPoints()-1;
1079 for(i=0;i<poly->GetNumPoints();i++) {
1080 vertices[i+polystartindex].p = poly->GetPoint(i);
1081 if(i==0) vertices[i+polystartindex].previous = polyendindex;
1082 else vertices[i+polystartindex].previous = i+polystartindex-1;
1083 if(i==(poly->GetNumPoints()-1)) vertices[i+polystartindex].next = polystartindex;
1084 else vertices[i+polystartindex].next = i+polystartindex+1;
1085 }
1086 polystartindex = polyendindex+1;
1087 }
1088
1089 //construct the priority queue
1090 long *priority = new long [numvertices];
1091 for(i=0;i<numvertices;i++) priority[i] = i;
1092 std::sort(priority,&(priority[numvertices]),VertexSorter(vertices));
1093
1094 //determine vertex types
1095 char *vertextypes = new char[maxnumvertices];
1096 for(i=0;i<numvertices;i++) {
1097 v = &(vertices[i]);
1098 vprev = &(vertices[v->previous]);
1099 vnext = &(vertices[v->next]);
1100
1101 if(Below(vprev->p,v->p)&&Below(vnext->p,v->p)) {
1102 if(IsConvex(vnext->p,vprev->p,v->p)) {
1103 vertextypes[i] = TPPL_VERTEXTYPE_START;
1104 } else {
1105 vertextypes[i] = TPPL_VERTEXTYPE_SPLIT;
1106 }
1107 } else if(Below(v->p,vprev->p)&&Below(v->p,vnext->p)) {
1108 if(IsConvex(vnext->p,vprev->p,v->p))
1109 {
1110 vertextypes[i] = TPPL_VERTEXTYPE_END;
1111 } else {
1112 vertextypes[i] = TPPL_VERTEXTYPE_MERGE;
1113 }
1114 } else {
1115 vertextypes[i] = TPPL_VERTEXTYPE_REGULAR;
1116 }
1117 }
1118
1119 //helpers
1120 long *helpers = new long[maxnumvertices];
1121
1122 //binary search tree that holds edges intersecting the scanline
1123 //note that while set doesn't actually have to be implemented as a tree
1124 //complexity requirements for operations are the same as for the balanced binary search tree
1125 set<ScanLineEdge> edgeTree;
1126 //store iterators to the edge tree elements
1127 //this makes deleting existing edges much faster
1128 set<ScanLineEdge>::iterator *edgeTreeIterators,edgeIter;
1129 edgeTreeIterators = new set<ScanLineEdge>::iterator[maxnumvertices];
1130 pair<set<ScanLineEdge>::iterator,bool> edgeTreeRet;
1131 for(i = 0; i<numvertices; i++) edgeTreeIterators[i] = edgeTree.end();
1132
1133 //for each vertex
1134 for(i=0;i<numvertices;i++) {
1135 vindex = priority[i];
1136 v = &(vertices[vindex]);
1137 vindex2 = vindex;
1138 v2 = v;
1139
1140 //depending on the vertex type, do the appropriate action
1141 //comments in the following sections are copied from "Computational Geometry: Algorithms and Applications"
1142 switch(vertextypes[vindex]) {
1143 case TPPL_VERTEXTYPE_START:
1144 //Insert ei in T and set helper(ei) to vi.
1145 newedge.p1 = v->p;
1146 newedge.p2 = vertices[v->next].p;
1147 newedge.index = vindex;
1148 edgeTreeRet = edgeTree.insert(newedge);
1149 edgeTreeIterators[vindex] = edgeTreeRet.first;
1150 helpers[vindex] = vindex;
1151 break;
1152
1153 case TPPL_VERTEXTYPE_END:
1154 //if helper(ei-1) is a merge vertex
1155 if(vertextypes[helpers[v->previous]]==TPPL_VERTEXTYPE_MERGE) {
1156 //Insert the diagonal connecting vi to helper(ei-1) in D.
1157 AddDiagonal(vertices,&newnumvertices,vindex,helpers[v->previous],
1158 vertextypes, edgeTreeIterators, &edgeTree, helpers);
1159 }
1160 //Delete ei-1 from T
1161 edgeTree.erase(edgeTreeIterators[v->previous]);
1162 break;
1163
1164 case TPPL_VERTEXTYPE_SPLIT:
1165 //Search in T to find the edge e j directly left of vi.
1166 newedge.p1 = v->p;
1167 newedge.p2 = v->p;
1168 edgeIter = edgeTree.lower_bound(newedge);
1169 if(edgeIter == edgeTree.begin()) {
1170 error = true;
1171 break;
1172 }
1173 edgeIter--;
1174 //Insert the diagonal connecting vi to helper(ej) in D.
1175 AddDiagonal(vertices,&newnumvertices,vindex,helpers[edgeIter->index],
1176 vertextypes, edgeTreeIterators, &edgeTree, helpers);
1177 vindex2 = newnumvertices-2;
1178 v2 = &(vertices[vindex2]);
1179 //helper(e j)�vi
1180 helpers[edgeIter->index] = vindex;
1181 //Insert ei in T and set helper(ei) to vi.
1182 newedge.p1 = v2->p;
1183 newedge.p2 = vertices[v2->next].p;
1184 newedge.index = vindex2;
1185 edgeTreeRet = edgeTree.insert(newedge);
1186 edgeTreeIterators[vindex2] = edgeTreeRet.first;
1187 helpers[vindex2] = vindex2;
1188 break;
1189
1190 case TPPL_VERTEXTYPE_MERGE:
1191 //if helper(ei-1) is a merge vertex
1192 if(vertextypes[helpers[v->previous]]==TPPL_VERTEXTYPE_MERGE) {
1193 //Insert the diagonal connecting vi to helper(ei-1) in D.
1194 AddDiagonal(vertices,&newnumvertices,vindex,helpers[v->previous],
1195 vertextypes, edgeTreeIterators, &edgeTree, helpers);
1196 vindex2 = newnumvertices-2;
1197 v2 = &(vertices[vindex2]);
1198 }
1199 //Delete ei-1 from T.
1200 edgeTree.erase(edgeTreeIterators[v->previous]);
1201 //Search in T to find the edge e j directly left of vi.
1202 newedge.p1 = v->p;
1203 newedge.p2 = v->p;
1204 edgeIter = edgeTree.lower_bound(newedge);
1205 if(edgeIter == edgeTree.begin()) {
1206 error = true;
1207 break;
1208 }
1209 edgeIter--;
1210 //if helper(ej) is a merge vertex
1211 if(vertextypes[helpers[edgeIter->index]]==TPPL_VERTEXTYPE_MERGE) {
1212 //Insert the diagonal connecting vi to helper(e j) in D.
1213 AddDiagonal(vertices,&newnumvertices,vindex2,helpers[edgeIter->index],
1214 vertextypes, edgeTreeIterators, &edgeTree, helpers);
1215 }
1216 //helper(e j)�vi
1217 helpers[edgeIter->index] = vindex2;
1218 break;
1219
1220 case TPPL_VERTEXTYPE_REGULAR:
1221 //if the interior of P lies to the right of vi
1222 if(Below(v->p,vertices[v->previous].p)) {
1223 //if helper(ei-1) is a merge vertex
1224 if(vertextypes[helpers[v->previous]]==TPPL_VERTEXTYPE_MERGE) {
1225 //Insert the diagonal connecting vi to helper(ei-1) in D.
1226 AddDiagonal(vertices,&newnumvertices,vindex,helpers[v->previous],
1227 vertextypes, edgeTreeIterators, &edgeTree, helpers);
1228 vindex2 = newnumvertices-2;
1229 v2 = &(vertices[vindex2]);
1230 }
1231 //Delete ei-1 from T.
1232 edgeTree.erase(edgeTreeIterators[v->previous]);
1233 //Insert ei in T and set helper(ei) to vi.
1234 newedge.p1 = v2->p;
1235 newedge.p2 = vertices[v2->next].p;
1236 newedge.index = vindex2;
1237 edgeTreeRet = edgeTree.insert(newedge);
1238 edgeTreeIterators[vindex2] = edgeTreeRet.first;
1239 helpers[vindex2] = vindex;
1240 } else {
1241 //Search in T to find the edge ej directly left of vi.
1242 newedge.p1 = v->p;
1243 newedge.p2 = v->p;
1244 edgeIter = edgeTree.lower_bound(newedge);
1245 if(edgeIter == edgeTree.begin()) {
1246 error = true;
1247 break;
1248 }
1249 edgeIter--;
1250 //if helper(ej) is a merge vertex
1251 if(vertextypes[helpers[edgeIter->index]]==TPPL_VERTEXTYPE_MERGE) {
1252 //Insert the diagonal connecting vi to helper(e j) in D.
1253 AddDiagonal(vertices,&newnumvertices,vindex,helpers[edgeIter->index],
1254 vertextypes, edgeTreeIterators, &edgeTree, helpers);
1255 }
1256 //helper(e j)�vi
1257 helpers[edgeIter->index] = vindex;
1258 }
1259 break;
1260 }
1261
1262 if(error) break;
1263 }
1264
1265 char *used = new char[newnumvertices];
1266 memset(used,0,newnumvertices*sizeof(char));
1267
1268 if(!error) {
1269 //return result
1270 long size;
1271 TPPLPoly mpoly;
1272 for(i=0;i<newnumvertices;i++) {
1273 if(used[i]) continue;
1274 v = &(vertices[i]);
1275 vnext = &(vertices[v->next]);
1276 size = 1;
1277 while(vnext!=v) {
1278 vnext = &(vertices[vnext->next]);
1279 size++;
1280 }
1281 mpoly.Init(size);
1282 v = &(vertices[i]);
1283 mpoly[0] = v->p;
1284 vnext = &(vertices[v->next]);
1285 size = 1;
1286 used[i] = 1;
1287 used[v->next] = 1;
1288 while(vnext!=v) {
1289 mpoly[size] = vnext->p;
1290 used[vnext->next] = 1;
1291 vnext = &(vertices[vnext->next]);
1292 size++;
1293 }
1294 monotonePolys->push_back(mpoly);
1295 }
1296 }
1297
1298 //cleanup
1299 delete [] vertices;
1300 delete [] priority;
1301 delete [] vertextypes;
1302 delete [] edgeTreeIterators;
1303 delete [] helpers;
1304 delete [] used;
1305
1306 if(error) {
1307 return 0;
1308 } else {
1309 return 1;
1310 }
1311 }
1312
1313 //adds a diagonal to the doubly-connected list of vertices
1314 void TPPLPartition::AddDiagonal(MonotoneVertex *vertices, long *numvertices, long index1, long index2,
1315 char *vertextypes, set<ScanLineEdge>::iterator *edgeTreeIterators,
1316 set<ScanLineEdge> *edgeTree, long *helpers)
1317 {
1318 long newindex1,newindex2;
1319
1320 newindex1 = *numvertices;
1321 (*numvertices)++;
1322 newindex2 = *numvertices;
1323 (*numvertices)++;
1324
1325 vertices[newindex1].p = vertices[index1].p;
1326 vertices[newindex2].p = vertices[index2].p;
1327
1328 vertices[newindex2].next = vertices[index2].next;
1329 vertices[newindex1].next = vertices[index1].next;
1330
1331 vertices[vertices[index2].next].previous = newindex2;
1332 vertices[vertices[index1].next].previous = newindex1;
1333
1334 vertices[index1].next = newindex2;
1335 vertices[newindex2].previous = index1;
1336
1337 vertices[index2].next = newindex1;
1338 vertices[newindex1].previous = index2;
1339
1340 //update all relevant structures
1341 vertextypes[newindex1] = vertextypes[index1];
1342 edgeTreeIterators[newindex1] = edgeTreeIterators[index1];
1343 helpers[newindex1] = helpers[index1];
1344 if(edgeTreeIterators[newindex1] != edgeTree->end())
1345 edgeTreeIterators[newindex1]->index = newindex1;
1346 vertextypes[newindex2] = vertextypes[index2];
1347 edgeTreeIterators[newindex2] = edgeTreeIterators[index2];
1348 helpers[newindex2] = helpers[index2];
1349 if(edgeTreeIterators[newindex2] != edgeTree->end())
1350 edgeTreeIterators[newindex2]->index = newindex2;
1351 }
1352
1353 bool TPPLPartition::Below(TPPLPoint &p1, TPPLPoint &p2) {
1354 if(p1.y < p2.y) return true;
1355 else if(p1.y == p2.y) {
1356 if(p1.x < p2.x) return true;
1357 }
1358 return false;
1359 }
1360
1361 //sorts in the falling order of y values, if y is equal, x is used instead
1362 bool TPPLPartition::VertexSorter::operator() (long index1, long index2) {
1363 if(vertices[index1].p.y > vertices[index2].p.y) return true;
1364 else if(vertices[index1].p.y == vertices[index2].p.y) {
1365 if(vertices[index1].p.x > vertices[index2].p.x) return true;
1366 }
1367 return false;
1368 }
1369
1370 bool TPPLPartition::ScanLineEdge::IsConvex(const TPPLPoint& p1, const TPPLPoint& p2, const TPPLPoint& p3) const {
1371 tppl_float tmp;
1372 tmp = (p3.y-p1.y)*(p2.x-p1.x)-(p3.x-p1.x)*(p2.y-p1.y);
1373 if(tmp>0) return 1;
1374 else return 0;
1375 }
1376
1377 bool TPPLPartition::ScanLineEdge::operator < (const ScanLineEdge & other) const {
1378 if(other.p1.y == other.p2.y) {
1379 if(p1.y == p2.y) {
1380 if(p1.y < other.p1.y) return true;
1381 else return false;
1382 }
1383 if(IsConvex(p1,p2,other.p1)) return true;
1384 else return false;
1385 } else if(p1.y == p2.y) {
1386 if(IsConvex(other.p1,other.p2,p1)) return false;
1387 else return true;
1388 } else if(p1.y < other.p1.y) {
1389 if(IsConvex(other.p1,other.p2,p1)) return false;
1390 else return true;
1391 } else {
1392 if(IsConvex(p1,p2,other.p1)) return true;
1393 else return false;
1394 }
1395 }
1396
1397 //triangulates monotone polygon
1398 //O(n) time, O(n) space complexity
1399 int TPPLPartition::TriangulateMonotone(TPPLPoly *inPoly, list<TPPLPoly> *triangles) {
1400 long i,i2,j,topindex,bottomindex,leftindex,rightindex,vindex;
1401 TPPLPoint *points;
1402 long numpoints;
1403 TPPLPoly triangle;
1404
1405 numpoints = inPoly->GetNumPoints();
1406 points = inPoly->GetPoints();
1407
1408 //trivial calses
1409 if(numpoints < 3) return 0;
1410 if(numpoints == 3) {
1411 triangles->push_back(*inPoly);
1412 }
1413
1414 topindex = 0; bottomindex=0;
1415 for(i=1;i<numpoints;i++) {
1416 if(Below(points[i],points[bottomindex])) bottomindex = i;
1417 if(Below(points[topindex],points[i])) topindex = i;
1418 }
1419
1420 //check if the poly is really monotone
1421 i = topindex;
1422 while(i!=bottomindex) {
1423 i2 = i+1; if(i2>=numpoints) i2 = 0;
1424 if(!Below(points[i2],points[i])) return 0;
1425 i = i2;
1426 }
1427 i = bottomindex;
1428 while(i!=topindex) {
1429 i2 = i+1; if(i2>=numpoints) i2 = 0;
1430 if(!Below(points[i],points[i2])) return 0;
1431 i = i2;
1432 }
1433
1434 char *vertextypes = new char[numpoints];
1435 long *priority = new long[numpoints];
1436
1437 //merge left and right vertex chains
1438 priority[0] = topindex;
1439 vertextypes[topindex] = 0;
1440 leftindex = topindex+1; if(leftindex>=numpoints) leftindex = 0;
1441 rightindex = topindex-1; if(rightindex<0) rightindex = numpoints-1;
1442 for(i=1;i<(numpoints-1);i++) {
1443 if(leftindex==bottomindex) {
1444 priority[i] = rightindex;
1445 rightindex--; if(rightindex<0) rightindex = numpoints-1;
1446 vertextypes[priority[i]] = -1;
1447 } else if(rightindex==bottomindex) {
1448 priority[i] = leftindex;
1449 leftindex++; if(leftindex>=numpoints) leftindex = 0;
1450 vertextypes[priority[i]] = 1;
1451 } else {
1452 if(Below(points[leftindex],points[rightindex])) {
1453 priority[i] = rightindex;
1454 rightindex--; if(rightindex<0) rightindex = numpoints-1;
1455 vertextypes[priority[i]] = -1;
1456 } else {
1457 priority[i] = leftindex;
1458 leftindex++; if(leftindex>=numpoints) leftindex = 0;
1459 vertextypes[priority[i]] = 1;
1460 }
1461 }
1462 }
1463 priority[i] = bottomindex;
1464 vertextypes[bottomindex] = 0;
1465
1466 long *stack = new long[numpoints];
1467 long stackptr = 0;
1468
1469 stack[0] = priority[0];
1470 stack[1] = priority[1];
1471 stackptr = 2;
1472
1473 //for each vertex from top to bottom trim as many triangles as possible
1474 for(i=2;i<(numpoints-1);i++) {
1475 vindex = priority[i];
1476 if(vertextypes[vindex]!=vertextypes[stack[stackptr-1]]) {
1477 for(j=0;j<(stackptr-1);j++) {
1478 if(vertextypes[vindex]==1) {
1479 triangle.Triangle(points[stack[j+1]],points[stack[j]],points[vindex]);
1480 } else {
1481 triangle.Triangle(points[stack[j]],points[stack[j+1]],points[vindex]);
1482 }
1483 triangles->push_back(triangle);
1484 }
1485 stack[0] = priority[i-1];
1486 stack[1] = priority[i];
1487 stackptr = 2;
1488 } else {
1489 stackptr--;
1490 while(stackptr>0) {
1491 if(vertextypes[vindex]==1) {
1492 if(IsConvex(points[vindex],points[stack[stackptr-1]],points[stack[stackptr]])) {
1493 triangle.Triangle(points[vindex],points[stack[stackptr-1]],points[stack[stackptr]]);
1494 triangles->push_back(triangle);
1495 stackptr--;
1496 } else {
1497 break;
1498 }
1499 } else {
1500 if(IsConvex(points[vindex],points[stack[stackptr]],points[stack[stackptr-1]])) {
1501 triangle.Triangle(points[vindex],points[stack[stackptr]],points[stack[stackptr-1]]);
1502 triangles->push_back(triangle);
1503 stackptr--;
1504 } else {
1505 break;
1506 }
1507 }
1508 }
1509 stackptr++;
1510 stack[stackptr] = vindex;
1511 stackptr++;
1512 }
1513 }
1514 vindex = priority[i];
1515 for(j=0;j<(stackptr-1);j++) {
1516 if(vertextypes[stack[j+1]]==1) {
1517 triangle.Triangle(points[stack[j]],points[stack[j+1]],points[vindex]);
1518 } else {
1519 triangle.Triangle(points[stack[j+1]],points[stack[j]],points[vindex]);
1520 }
1521 triangles->push_back(triangle);
1522 }
1523
1524 delete [] priority;
1525 delete [] vertextypes;
1526 delete [] stack;
1527
1528 return 1;
1529 }
1530
1531 int TPPLPartition::Triangulate_MONO(list<TPPLPoly> *inpolys, list<TPPLPoly> *triangles) {
1532 list<TPPLPoly> monotone;
1533 list<TPPLPoly>::iterator iter;
1534
1535 if(!MonotonePartition(inpolys,&monotone)) return 0;
1536 for(iter = monotone.begin(); iter!=monotone.end();iter++) {
1537 if(!TriangulateMonotone(&(*iter),triangles)) return 0;
1538 }
1539 return 1;
1540 }
1541
1542 int TPPLPartition::Triangulate_MONO(TPPLPoly *poly, list<TPPLPoly> *triangles) {
1543 list<TPPLPoly> polys;
1544 polys.push_back(*poly);
1545
1546 return Triangulate_MONO(&polys, triangles);
1547 }
Show file before | Show file after | Hide comments
@@ -0,0 +1,350
1 //Copyright (C) 2011 by Ivan Fratric
2 //
3 //Permission is hereby granted, free of charge, to any person obtaining a copy
4 //of this software and associated documentation files (the "Software"), to deal
5 //in the Software without restriction, including without limitation the rights
6 //to use, copy, modify, merge, publish, distribute, sublicense, and/or sell
7 //copies of the Software, and to permit persons to whom the Software is
8 //furnished to do so, subject to the following conditions:
9 //
10 //The above copyright notice and this permission notice shall be included in
11 //all copies or substantial portions of the Software.
12 //
13 //THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
14 //IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
15 //FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
16 //AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
17 //LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
18 //OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN
19 //THE SOFTWARE.
20
21 #ifndef POLYPARTITION_H
22 #define POLYPARTITION_H
23
24 #include <list>
25 #include <set>
26
27 typedef double tppl_float;
28
29 #define TPPL_CCW 1
30 #define TPPL_CW -1
31
32 //2D point structure
33 struct TPPLPoint {
34 tppl_float x;
35 tppl_float y;
36
37 TPPLPoint operator + (const TPPLPoint& p) const {
38 TPPLPoint r;
39 r.x = x + p.x;
40 r.y = y + p.y;
41 return r;
42 }
43
44 TPPLPoint operator - (const TPPLPoint& p) const {
45 TPPLPoint r;
46 r.x = x - p.x;
47 r.y = y - p.y;
48 return r;
49 }
50
51 TPPLPoint operator * (const tppl_float f ) const {
52 TPPLPoint r;
53 r.x = x*f;
54 r.y = y*f;
55 return r;
56 }
57
58 TPPLPoint operator / (const tppl_float f ) const {
59 TPPLPoint r;
60 r.x = x/f;
61 r.y = y/f;
62 return r;
63 }
64
65 bool operator==(const TPPLPoint& p) const {
66 if((x == p.x)&&(y==p.y)) return true;
67 else return false;
68 }
69
70 bool operator!=(const TPPLPoint& p) const {
71 if((x == p.x)&&(y==p.y)) return false;
72 else return true;
73 }
74 };
75
76 //Polygon implemented as an array of points with a 'hole' flag
77 class TPPLPoly {
78 protected:
79
80 TPPLPoint *points;
81 long numpoints;
82 bool hole;
83
84 public:
85
86 //constructors/destructors
87 TPPLPoly();
88 ~TPPLPoly();
89
90 TPPLPoly(const TPPLPoly &src);
91 TPPLPoly& operator=(const TPPLPoly &src);
92
93 //getters and setters
94 long GetNumPoints() {
95 return numpoints;
96 }
97
98 bool IsHole() {
99 return hole;
100 }
101
102 void SetHole(bool hole) {
103 this->hole = hole;
104 }
105
106 TPPLPoint &GetPoint(long i) {
107 return points[i];
108 }
109
110 TPPLPoint *GetPoints() {
111 return points;
112 }
113
114 TPPLPoint& operator[] (int i) {
115 return points[i];
116 }
117
118 //clears the polygon points
119 void Clear();
120
121 //inits the polygon with numpoints vertices
122 void Init(long numpoints);
123
124 //creates a triangle with points p1,p2,p3
125 void Triangle(TPPLPoint &p1, TPPLPoint &p2, TPPLPoint &p3);
126
127 //inverts the orfer of vertices
128 void Invert();
129
130 //returns the orientation of the polygon
131 //possible values:
132 // TPPL_CCW : polygon vertices are in counter-clockwise order
133 // TPPL_CW : polygon vertices are in clockwise order
134 // 0 : the polygon has no (measurable) area
135 int GetOrientation();
136
137 //sets the polygon orientation
138 //orientation can be
139 // TPPL_CCW : sets vertices in counter-clockwise order
140 // TPPL_CW : sets vertices in clockwise order
141 void SetOrientation(int orientation);
142 };
143
144 class TPPLPartition {
145 protected:
146 struct PartitionVertex {
147 bool isActive;
148 bool isConvex;
149 bool isEar;
150
151 TPPLPoint p;
152 tppl_float angle;
153 PartitionVertex *previous;
154 PartitionVertex *next;
155 };
156
157 struct MonotoneVertex {
158 TPPLPoint p;
159 long previous;
160 long next;
161 };
162
163 class VertexSorter{
164 MonotoneVertex *vertices;
165 public:
166 VertexSorter(MonotoneVertex *v) : vertices(v) {}
167 bool operator() (long index1, long index2);
168 };
169
170 struct Diagonal {
171 long index1;
172 long index2;
173 };
174
175 //dynamic programming state for minimum-weight triangulation
176 struct DPState {
177 bool visible;
178 tppl_float weight;
179 long bestvertex;
180 };
181
182 //dynamic programming state for convex partitioning
183 struct DPState2 {
184 bool visible;
185 long weight;
186 std::list<Diagonal> pairs;
187 };
188
189 //edge that intersects the scanline
190 struct ScanLineEdge {
191 mutable long index;
192 TPPLPoint p1;
193 TPPLPoint p2;
194
195 //determines if the edge is to the left of another edge
196 bool operator< (const ScanLineEdge & other) const;
197
198 bool IsConvex(const TPPLPoint& p1, const TPPLPoint& p2, const TPPLPoint& p3) const;
199 };
200
201 //standard helper functions
202 bool IsConvex(TPPLPoint& p1, TPPLPoint& p2, TPPLPoint& p3);
203 bool IsReflex(TPPLPoint& p1, TPPLPoint& p2, TPPLPoint& p3);
204 bool IsInside(TPPLPoint& p1, TPPLPoint& p2, TPPLPoint& p3, TPPLPoint &p);
205
206 bool InCone(TPPLPoint &p1, TPPLPoint &p2, TPPLPoint &p3, TPPLPoint &p);
207 bool InCone(PartitionVertex *v, TPPLPoint &p);
208
209 int Intersects(TPPLPoint &p11, TPPLPoint &p12, TPPLPoint &p21, TPPLPoint &p22);
210
211 TPPLPoint Normalize(const TPPLPoint &p);
212 tppl_float Distance(const TPPLPoint &p1, const TPPLPoint &p2);
213
214 //helper functions for Triangulate_EC
215 void UpdateVertexReflexity(PartitionVertex *v);
216 void UpdateVertex(PartitionVertex *v,PartitionVertex *vertices, long numvertices);
217
218 //helper functions for ConvexPartition_OPT
219 void UpdateState(long a, long b, long w, long i, long j, DPState2 **dpstates);
220 void TypeA(long i, long j, long k, PartitionVertex *vertices, DPState2 **dpstates);
221 void TypeB(long i, long j, long k, PartitionVertex *vertices, DPState2 **dpstates);
222
223 //helper functions for MonotonePartition
224 bool Below(TPPLPoint &p1, TPPLPoint &p2);
225 void AddDiagonal(MonotoneVertex *vertices, long *numvertices, long index1, long index2,
226 char *vertextypes, std::set<ScanLineEdge>::iterator *edgeTreeIterators,
227 std::set<ScanLineEdge> *edgeTree, long *helpers);
228
229 //triangulates a monotone polygon, used in Triangulate_MONO
230 int TriangulateMonotone(TPPLPoly *inPoly, std::list<TPPLPoly> *triangles);
231
232 public:
233
234 //simple heuristic procedure for removing holes from a list of polygons
235 //works by creating a diagonal from the rightmost hole vertex to some visible vertex
236 //time complexity: O(h*(n^2)), h is the number of holes, n is the number of vertices
237 //space complexity: O(n)
238 //params:
239 // inpolys : a list of polygons that can contain holes
240 // vertices of all non-hole polys have to be in counter-clockwise order
241 // vertices of all hole polys have to be in clockwise order
242 // outpolys : a list of polygons without holes
243 //returns 1 on success, 0 on failure
244 int RemoveHoles(std::list<TPPLPoly> *inpolys, std::list<TPPLPoly> *outpolys);
245
246 //triangulates a polygon by ear clipping
247 //time complexity O(n^2), n is the number of vertices
248 //space complexity: O(n)
249 //params:
250 // poly : an input polygon to be triangulated
251 // vertices have to be in counter-clockwise order
252 // triangles : a list of triangles (result)
253 //returns 1 on success, 0 on failure
254 int Triangulate_EC(TPPLPoly *poly, std::list<TPPLPoly> *triangles);
255
256 //triangulates a list of polygons that may contain holes by ear clipping algorithm
257 //first calls RemoveHoles to get rid of the holes, and then Triangulate_EC for each resulting polygon
258 //time complexity: O(h*(n^2)), h is the number of holes, n is the number of vertices
259 //space complexity: O(n)
260 //params:
261 // inpolys : a list of polygons to be triangulated (can contain holes)
262 // vertices of all non-hole polys have to be in counter-clockwise order
263 // vertices of all hole polys have to be in clockwise order
264 // triangles : a list of triangles (result)
265 //returns 1 on success, 0 on failure
266 int Triangulate_EC(std::list<TPPLPoly> *inpolys, std::list<TPPLPoly> *triangles);
267
268 //creates an optimal polygon triangulation in terms of minimal edge length
269 //time complexity: O(n^3), n is the number of vertices
270 //space complexity: O(n^2)
271 //params:
272 // poly : an input polygon to be triangulated
273 // vertices have to be in counter-clockwise order
274 // triangles : a list of triangles (result)
275 //returns 1 on success, 0 on failure
276 int Triangulate_OPT(TPPLPoly *poly, std::list<TPPLPoly> *triangles);
277
278 //triangulates a polygons by firstly partitioning it into monotone polygons
279 //time complexity: O(n*log(n)), n is the number of vertices
280 //space complexity: O(n)
281 //params:
282 // poly : an input polygon to be triangulated
283 // vertices have to be in counter-clockwise order
284 // triangles : a list of triangles (result)
285 //returns 1 on success, 0 on failure
286 int Triangulate_MONO(TPPLPoly *poly, std::list<TPPLPoly> *triangles);
287
288 //triangulates a list of polygons by firstly partitioning them into monotone polygons
289 //time complexity: O(n*log(n)), n is the number of vertices
290 //space complexity: O(n)
291 //params:
292 // inpolys : a list of polygons to be triangulated (can contain holes)
293 // vertices of all non-hole polys have to be in counter-clockwise order
294 // vertices of all hole polys have to be in clockwise order
295 // triangles : a list of triangles (result)
296 //returns 1 on success, 0 on failure
297 int Triangulate_MONO(std::list<TPPLPoly> *inpolys, std::list<TPPLPoly> *triangles);
298
299 //creates a monotone partition of a list of polygons that can contain holes
300 //time complexity: O(n*log(n)), n is the number of vertices
301 //space complexity: O(n)
302 //params:
303 // inpolys : a list of polygons to be triangulated (can contain holes)
304 // vertices of all non-hole polys have to be in counter-clockwise order
305 // vertices of all hole polys have to be in clockwise order
306 // monotonePolys : a list of monotone polygons (result)
307 //returns 1 on success, 0 on failure
308 int MonotonePartition(std::list<TPPLPoly> *inpolys, std::list<TPPLPoly> *monotonePolys);
309
310 //partitions a polygon into convex polygons by using Hertel-Mehlhorn algorithm
311 //the algorithm gives at most four times the number of parts as the optimal algorithm
312 //however, in practice it works much better than that and often gives optimal partition
313 //uses triangulation obtained by ear clipping as intermediate result
314 //time complexity O(n^2), n is the number of vertices
315 //space complexity: O(n)
316 //params:
317 // poly : an input polygon to be partitioned
318 // vertices have to be in counter-clockwise order
319 // parts : resulting list of convex polygons
320 //returns 1 on success, 0 on failure
321 int ConvexPartition_HM(TPPLPoly *poly, std::list<TPPLPoly> *parts);
322
323 //partitions a list of polygons into convex parts by using Hertel-Mehlhorn algorithm
324 //the algorithm gives at most four times the number of parts as the optimal algorithm
325 //however, in practice it works much better than that and often gives optimal partition
326 //uses triangulation obtained by ear clipping as intermediate result
327 //time complexity O(n^2), n is the number of vertices
328 //space complexity: O(n)
329 //params:
330 // inpolys : an input list of polygons to be partitioned
331 // vertices of all non-hole polys have to be in counter-clockwise order
332 // vertices of all hole polys have to be in clockwise order
333 // parts : resulting list of convex polygons
334 //returns 1 on success, 0 on failure
335 int ConvexPartition_HM(std::list<TPPLPoly> *inpolys, std::list<TPPLPoly> *parts);
336
337 //optimal convex partitioning (in terms of number of resulting convex polygons)
338 //using the Keil-Snoeyink algorithm
339 //M. Keil, J. Snoeyink, "On the time bound for convex decomposition of simple polygons", 1998
340 //time complexity O(n^3), n is the number of vertices
341 //space complexity: O(n^3)
342 // poly : an input polygon to be partitioned
343 // vertices have to be in counter-clockwise order
344 // parts : resulting list of convex polygons
345 //returns 1 on success, 0 on failure
346 int ConvexPartition_OPT(TPPLPoly *poly, std::list<TPPLPoly> *parts);
347 };
348
349
350 #endif
Show file before | Show file after | Hide comments
@@ -0,0 +1,351
1 //Copyright (C) 2011 by Ivan Fratric
2 //
3 //Permission is hereby granted, free of charge, to any person obtaining a copy
4 //of this software and associated documentation files (the "Software"), to deal
5 //in the Software without restriction, including without limitation the rights
6 //to use, copy, modify, merge, publish, distribute, sublicense, and/or sell
7 //copies of the Software, and to permit persons to whom the Software is
8 //furnished to do so, subject to the following conditions:
9 //
10 //The above copyright notice and this permission notice shall be included in
11 //all copies or substantial portions of the Software.
12 //
13 //THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
14 //IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
15 //FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
16 //AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
17 //LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
18 //OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN
19 //THE SOFTWARE.
20
21
22 #include <stdio.h>
23 #include <stdlib.h>
24 #include <string.h>
25 #include <math.h>
26
27 #include "image.h"
28
29 Image::Image(void)
30 {
31 width = 0;
32 height = 0;
33 data = NULL;
34 }
35
36 Image::Image(long width, long height)
37 {
38 this->width = width;
39 this->height = height;
40 data = (unsigned char *)malloc(3*width*height);
41 memset(data,0,3*width*height);
42 }
43
44 Image::Image(const Image& src) {
45 width = src.width;
46 height = src.height;
47 data = (unsigned char *)malloc(3*width*height);
48 memcpy(data,src.data,3*width*height);
49 }
50
51 Image& Image::operator=(const Image &src) {
52 width = src.width;
53 height = src.height;
54 if(data) free(data);
55 data = (unsigned char *)malloc(3*width*height);
56 memcpy(data,src.data,3*width*height);
57 return *this;
58 }
59
60 Image::~Image(void)
61 {
62 if(data) free(data);
63 }
64
65 void Image::Init(long width, long height)
66 {
67 if(data) free(data);
68 this->width = width;
69 this->height = height;
70 data = (unsigned char *)malloc(3*width*height);
71 memset(data,0,3*width*height);
72 }
73
74 unsigned char Image::GetMeanGray() {
75 long sum = 0;
76 for(long i = 0; i <height; i++) {
77 for(long j = 0; j<width;j++) {
78 sum += GetPixelGray(j,i);
79 }
80 }
81 return (unsigned char)(sum/(width*height));
82 }
83
84 void Image::Binarize(unsigned char threshold) {
85 unsigned char c;
86 for(long i = 0; i <height; i++) {
87 for(long j = 0; j<width;j++) {
88 c = GetPixelGray(j,i);
89 if(c > threshold) {
90 SetPixelGray(j,i,255);
91 } else {
92 SetPixelGray(j,i,0);
93 }
94 }
95 }
96 }
97
98 void Image::FlipHorizontal() {
99 unsigned char *newdata;
100 newdata = (unsigned char *)malloc(height*width*3);
101 for(long i = 0; i <height; i++) {
102 for(long j = 0; j<width;j++) {
103 long index1 = 3*((i*width)+j);
104 long index2 = 3*((i*width)+width-j-1);
105 newdata[index1] = data[index2];
106 index1++; index2++;
107 newdata[index1] = data[index2];
108 index1++; index2++;
109 newdata[index1] = data[index2];
110 index1++; index2++;
111 }
112 }
113 free(data);
114 data = newdata;
115 }
116
117 void Image::FlipVertical() {
118 unsigned char *newdata;
119 newdata = (unsigned char *)malloc(height*width*3);
120 for(long i = 0; i <height; i++) {
121 for(long j = 0; j<width;j++) {
122 long index1 = 3*((i*width)+j);
123 long index2 = 3*(((height-i-1)*width)+j);
124 newdata[index1] = data[index2];
125 index1++; index2++;
126 newdata[index1] = data[index2];
127 index1++; index2++;
128 newdata[index1] = data[index2];
129 index1++; index2++;
130 }
131 }
132 free(data);
133 data = newdata;
134 }
135
136 Image::Pixel Image::GetPixelBilinear(float x, float y) {
137 Image::Pixel c={0,0,0},c1,c2,c3,c4;
138 if(x<0) return c;
139 if(y<0) return c;
140 if(x>(width-1)) return c;
141 if(y>(height-1)) return c;
142 long x1,y1;
143 float dx,dy;
144 x1=(long)floor(x);
145 y1=(long)floor(y);
146 dx=x-x1;
147 dy=y-y1;
148 c1=GetPixelColor(x1,y1);
149 c2=GetPixelColor(x1+1,y1);
150 c3=GetPixelColor(x1,y1+1);
151 c4=GetPixelColor(x1+1,y1+1);
152 c.R=(unsigned char)round(interpolate(c1.R,c2.R,c3.R,c4.R,dx,dy));
153 c.G=(unsigned char)round(interpolate(c1.G,c2.G,c3.G,c4.G,dx,dy));
154 c.B=(unsigned char)round(interpolate(c1.B,c2.B,c3.B,c4.B,dx,dy));
155 return(c);
156 }
157
158 float Image::interpolate(float x1,float x2,float x3, float x4, float dx, float dy) {
159 float x5,x6;
160 x5=x2*dx+x1*(1-dx);
161 x6=x4*dx+x3*(1-dx);
162 return(x6*dy+x5*(1-dy));
163 }
164
165 long Image::round(float x) {
166 if((x-floor(x))<0.5) return (long)floor(x);
167 else return (long)ceil(x);
168 }
169
170 void Image::GetHistogramGray(long *histogram) {
171 for(long i =0;i<256;i++) histogram[i] = 0;
172 for(long i = 0; i <height; i++) {
173 for(long j = 0; j<width;j++) {
174 histogram[GetPixelGray(j,i)]++;
175 }
176 }
177 }
178
179 void Image::Invert() {
180 long i,n = 3*width*height;
181 for(i=0;i<n;i++) {
182 data[i]=255-data[i];
183 }
184 }
185
186 Image Image::Crop(int posx, int posy, int width, int height) {
187 Image resultimg;
188 Image::Pixel rgb;
189 resultimg.Init(width,height);
190 long i,j;
191 for(i=0;i<height;i++) {
192 for(j=0;j<width;j++) {
193 rgb = this->GetPixelColor(j+posx,i+posy);
194 resultimg.SetPixelColor(j,i,rgb);
195 }
196 }
197 return resultimg;
198 }
199
200 Image Image::Resize(int factor) {
201 long width,height;
202 int factor2;
203 long sumR, sumG, sumB;
204
205 width = this->width / factor;
206 height = this->height / factor;
207 factor2 = factor*factor;
208
209 Image resultimg(width,height);
210 Image::Pixel rgb;
211 long i,j,i2,j2,minx,miny,maxx,maxy;
212
213 for(i=0;i<height;i++) {
214 for(j=0;j<width;j++) {
215 minx = j*factor;
216 miny = i*factor;
217 maxx = minx+factor;
218 maxy = miny+factor;
219
220 sumR = 0; sumG = 0; sumB = 0;
221
222 for(i2=miny;i2<maxy;i2++) {
223 for(j2=minx;j2<maxx;j2++) {
224 rgb = GetPixelColor(j2,i2);
225 sumR += rgb.R;
226 sumG += rgb.G;
227 sumB += rgb.B;
228 }
229 }
230 rgb.R = (unsigned char)round(sumR/((float)factor2));
231 rgb.G = (unsigned char)round(sumG/((float)factor2));
232 rgb.B = (unsigned char)round(sumB/((float)factor2));
233 resultimg.SetPixelColor(j,i,rgb);
234 }
235 }
236 return resultimg;
237 }
238
239 Image Image::Filter(float *filter, long filterwidth, long filterheight) {
240 Image ret(width,height);
241 long i1,j1,i2,j2;
242 long fox,foy,filtersize;
243 long x,y;
244 float sumr,sumg,sumb;
245 long offset1,offset2,offset3;
246 unsigned char *data1,*data2;
247 fox = filterwidth/2;
248 foy = filterheight/2;
249 filtersize = filterwidth*filterheight;
250 data1 = ret.GetData();
251 data2 = data;
252 for(i1=0;i1<height;i1++) {
253 for(j1=0;j1<width;j1++) {
254 offset1 = (i1*width+j1)*3;
255 sumr = 0;
256 sumg = 0;
257 sumb = 0;
258 for(i2=-foy;i2<=foy;i2++) {
259 for(j2=-fox;j2<=fox;j2++) {
260 x = j1+j2;
261 y = i1+i2;
262 if(x<0) x = 0;
263 if(y<0) y = 0;
264 if(x>=width) x = width-1;
265 if(y>=height) y = height-1;
266 offset2 = (y*width+x)*3;
267 offset3 = (i2+foy)*filterwidth+j2+fox;
268 sumr += data2[offset2]*filter[offset3];
269 sumg += data2[offset2+1]*filter[offset3];
270 sumb += data2[offset2+2]*filter[offset3];
271 }
272 }
273 data1[offset1] = (unsigned char)round(sumr);
274 data1[offset1+1] = (unsigned char)round(sumg);
275 data1[offset1+2] = (unsigned char)round(sumb);
276 }
277 }
278 return ret;
279 }
280
281 Image Image::GaussBlur(float sigma, long masksize) {
282 Image ret;
283 float *filter;
284 long fsize;
285 long i,j;
286 long fo;
287 float pi = 3.1415926538f;
288
289 if(!masksize) masksize = round(sigma)*2*2+1;
290
291 fsize = masksize*masksize;
292 fo = masksize/2;
293 filter = (float *)malloc(fsize*sizeof(float));
294
295 for(i=-fo;i<=fo;i++) {
296 for(j=-fo;j<=fo;j++) {
297 filter[(i+fo)*masksize+j+fo] = (1/(2*pi*sigma))*exp(-(i*i+j*j)/(2*sigma*sigma));
298 }
299 }
300
301 float sum = 0;
302 for(i=0;i<fsize;i++) sum += filter[i];
303 for(i=0;i<fsize;i++) filter[i]=filter[i]/sum;
304
305 ret = this->Filter(filter,masksize,masksize);
306
307 delete filter;
308 return ret;
309 }
310
311 void Image::Clear(Pixel color) {
312 long x,y;
313 for(y=0;y<height;y++) {
314 for(x=0;x<width;x++) {
315 SetPixelColor(x,y,color);
316 }
317 }
318 }
319
320 void Image::DrawLine(int x1, int y1, int x2, int y2, Pixel color) {
321 long i;
322 long y;
323 long dx,dy;
324 dx=labs(x2-x1);
325 dy=labs(y2-y1);
326 if(dx>dy) {
327 if(x2>x1) {
328 for(i=x1;i<=x2;i++) {
329 y=(long)(((y2-(float)(y1))/(x2-x1))*(i-x1)+y1);
330 SetPixelColor(i,y,color);
331 }
332 } else {
333 for(i=x2;i<=x1;i++) {
334 y=(long)(((y1-(float)(y2))/(x1-x2))*(i-x2)+y2);
335 SetPixelColor(i,y,color);
336 }
337 }
338 } else {
339 if(y2>y1) {
340 for(i=y1;i<=y2;i++) {
341 y=(long)(((x2-(float)(x1))/(y2-y1))*(i-y1)+x1);
342 SetPixelColor(y,i,color);
343 }
344 } else {
345 for(i=y2;i<=y1;i++) {
346 y=(long)(((x1-(float)(x2))/(y1-y2))*(i-y2)+x2);
347 SetPixelColor(y,i,color);
348 }
349 }
350 }
351 }
Show file before | Show file after | Hide comments
@@ -0,0 +1,211
1 //Copyright (C) 2011 by Ivan Fratric
2 //
3 //Permission is hereby granted, free of charge, to any person obtaining a copy
4 //of this software and associated documentation files (the "Software"), to deal
5 //in the Software without restriction, including without limitation the rights
6 //to use, copy, modify, merge, publish, distribute, sublicense, and/or sell
7 //copies of the Software, and to permit persons to whom the Software is
8 //furnished to do so, subject to the following conditions:
9 //
10 //The above copyright notice and this permission notice shall be included in
11 //all copies or substantial portions of the Software.
12 //
13 //THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
14 //IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
15 //FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
16 //AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
17 //LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
18 //OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN
19 //THE SOFTWARE.
20
21
22 #pragma once
23
24 //a simple image class with some (very basic) image processing operations
25 class Image
26 {
27 friend class ImageIO;
28
29 protected:
30 unsigned char *data;
31 long width;
32 long height;
33
34 long round(float x);
35 float interpolate(float x1,float x2,float x3, float x4, float dx, float dy);
36
37 public:
38
39 struct Pixel {
40 unsigned char B;
41 unsigned char G;
42 unsigned char R;
43 };
44
45 //constructors/destructor
46 Image(void);
47 Image(long width, long height);
48 Image(const Image& src);
49 Image& operator=(const Image &src);
50 ~Image(void);
51
52 //initializes the image of specified width and height
53 //all pixels are set to black
54 void Init(long width, long height);
55
56 //property getters
57 long GetWidth();
58 long GetHeight();
59 unsigned char *GetData();
60
61 //pixel getters and setters
62 unsigned char GetPixelGray(long x,long y);
63 unsigned char GetPixelRed(long x,long y);
64 unsigned char GetPixelGreen(long x,long y);
65 unsigned char GetPixelBlue(long x,long y);
66 Image::Pixel GetPixelColor(long x,long y);
67 void SetPixelGray(long x,long y, unsigned char c);
68 void SetPixelColor(long x,long y, Image::Pixel rgb);
69 void SetPixelRed(long x,long y, unsigned char c);
70 void SetPixelGreen(long x,long y, unsigned char c);
71 void SetPixelBlue(long x,long y, unsigned char c);
72
73 //returns the color of a pixel at real coordinates (x,y)
74 //using bilinear interpolation
75 Image::Pixel GetPixelBilinear(float x, float y);
76
77 /////////////////////////////////////////
78 //some basic image processing functions//
79 /////////////////////////////////////////
80
81 //returns the mean value of pixel intensity
82 unsigned char GetMeanGray();
83
84 //computes the histogram of image intensity and returns it via histogram parameter
85 //parameters:
86 // histogram : an array of 256 components, used to return the histogram
87 void GetHistogramGray(long *histogram);
88
89 //binarizes the image
90 //all pixels with the intensity lower than threshold become black
91 //all others become white
92 void Binarize(unsigned char threshold);
93
94 //flips the image in horizontal direction
95 void FlipHorizontal();
96
97 //flips the image in vertical direction
98 void FlipVertical();
99
100 //inverts image colors
101 void Invert();
102
103 //crops the image
104 //returns the subimage with upper left corner at (posx,posy)
105 //the returned image is of size (width, height)
106 Image Crop(int posx, int posy, int width, int height);
107
108 //resizes the image for a intager facor
109 //for example, if factor is 2, returns the image with size (width/2, height/2)
110 //each pixel in a new image is obtained as an average of corresponding pixels in the original image
111 Image Resize(int factor);
112
113 //computes the convolution of image and a filter
114 //parameters
115 // filter : an filterwidth x filterheight array containing the filter coefficients
116 // filterwidth : width of the filter
117 // filterheight : height of the filter
118 // zero : a value that will be added to each pixel component after filtering, 0 by default
119 Image Filter(float *filter, long filterwidth, long filterheight);
120
121 //filters the image using Gaussian blur
122 //parameters
123 // sigma : the standard deviation of the Gaussian filter
124 // masksize : the size of the corresponding filter
125 // if set to 0, the masksize will be calculated as sigma*2*2+1
126 Image GaussBlur(float sigma, long masksize = 0);
127
128 //paints the whole image with color 'color'
129 void Clear(Pixel color);
130
131 //draws a line from point (x1,y1) to point (x2,y2)
132 //the line is in color 'color'
133 void DrawLine(int x1, int y1, int x2, int y2, Pixel color);
134 };
135
136 inline unsigned char Image::GetPixelGray(long x,long y) {
137 unsigned char c;
138 long index = 3*((y*width)+x);
139 c = (unsigned char)(((long)(data[index])+(long)(data[index+1])+(long)(data[index+2]))/3);
140 return c;
141 }
142
143 inline unsigned char Image::GetPixelRed(long x,long y) {
144 long index = 3*((y*width)+x);
145 return data[index];
146 }
147
148 inline unsigned char Image::GetPixelGreen(long x,long y) {
149 long index = 3*((y*width)+x)+1;
150 return data[index];
151 }
152
153 inline unsigned char Image::GetPixelBlue(long x,long y) {
154 long index = 3*((y*width)+x)+2;
155 return data[index];
156 }
157
158 inline void Image::SetPixelRed(long x,long y, unsigned char c) {
159 long index = 3*((y*width)+x);
160 data[index]=c;
161 }
162
163 inline void Image::SetPixelGreen(long x,long y, unsigned char c) {
164 long index = 3*((y*width)+x)+1;
165 data[index]=c;
166 }
167
168 inline void Image::SetPixelBlue(long x,long y, unsigned char c) {
169 long index = 3*((y*width)+x)+2;
170 data[index]=c;
171 }
172
173 inline Image::Pixel Image::GetPixelColor(long x,long y) {
174 Image::Pixel rgb;
175 long index = 3*((y*width)+x);
176 rgb.B = data[index];
177 rgb.G = data[index+1];
178 rgb.R = data[index+2];
179 return rgb;
180 }
181
182 inline void Image::SetPixelGray(long x,long y, unsigned char c) {
183 long index = 3*((y*width)+x);
184 data[index] = c;
185 data[index+1] = c;
186 data[index+2] = c;
187 }
188
189 inline void Image::SetPixelColor(long x,long y, Image::Pixel rgb) {
190 if(x<0) return;
191 if(y<0) return;
192 if(x>=width) return;
193 if(y>=height) return;
194 long index = 3*((y*width)+x);
195 data[index] = rgb.B;
196 data[index+1] = rgb.G;
197 data[index+2] = rgb.R;
198 }
199
200 inline long Image::GetWidth() {
201 return width;
202 }
203
204 inline long Image::GetHeight() {
205 return height;
206 }
207
208 inline unsigned char *Image::GetData() {
209 return data;
210 }
211
Show file before | Show file after | Hide comments
@@ -0,0 +1,496
1 //Copyright (C) 2011 by Ivan Fratric
2 //
3 //Permission is hereby granted, free of charge, to any person obtaining a copy
4 //of this software and associated documentation files (the "Software"), to deal
5 //in the Software without restriction, including without limitation the rights
6 //to use, copy, modify, merge, publish, distribute, sublicense, and/or sell
7 //copies of the Software, and to permit persons to whom the Software is
8 //furnished to do so, subject to the following conditions:
9 //
10 //The above copyright notice and this permission notice shall be included in
11 //all copies or substantial portions of the Software.
12 //
13 //THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
14 //IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
15 //FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
16 //AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
17 //LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
18 //OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN
19 //THE SOFTWARE.
20
21 #define _CRT_SECURE_NO_WARNINGS
22
23 #include <stdio.h>
24 #include <stdlib.h>
25 #include <string.h>
26
27 #include <math.h>
28
29 #include "image.h"
30 #include "imageio.h"
31
32 const char *ImageIO::GetFileExtension(const char *filename) {
33 //first remove the folder if present
34 const char *filename2,*tmp,*extension;
35 filename2 = strrchr(filename,'/');
36 tmp = strrchr(filename,'\\');
37 if(tmp > filename2) filename2 = tmp;
38 if(!filename2) filename2 = filename;
39 //now find the dot
40 extension = strrchr(filename2,'.');
41 if(extension) extension++;
42 else extension = filename2 + strlen(filename2);
43 return extension;
44 }
45
46 int ImageIO::GetImageType(const char *filename) {
47 const char *extension = GetFileExtension(filename);
48 if((strcmp(extension,"bmp")==0)||(strcmp(extension,"BMP")==0)) {
49 return IMGTYPE_BMP;
50 } else if((strcmp(extension,"ppm")==0)||(strcmp(extension,"PPM")==0)) {
51 return IMGTYPE_PPM;
52 } else if((strcmp(extension,"pgm")==0)||(strcmp(extension,"PGM")==0)) {
53 return IMGTYPE_PGM;
54 } else if((strcmp(extension,"raw")==0)||(strcmp(extension,"RAW")==0)) {
55 return IMGTYPE_RAW;
56 } else return IMGTYPE_UNSUPPORTED;
57 }
58
59 void ImageIO::LoadImage(const char *filename, Image *image) {
60 int imgType = GetImageType(filename);
61 if(imgType == IMGTYPE_UNSUPPORTED) {
62 printf("Error loading image %s, unsupported image type!\n", filename);
63 return;
64 }
65 LoadImage(filename, image, imgType);
66 }
67
68 void ImageIO::LoadImage(const char *filename, Image *image, int imageType) {
69 switch(imageType) {
70 case IMGTYPE_BMP:
71 LoadImageBMP(filename, image);
72 break;
73 case IMGTYPE_PPM:
74 LoadImagePPM(filename, image);
75 break;
76 case IMGTYPE_PGM:
77 LoadImagePGM(filename, image);
78 break;
79 case IMGTYPE_RAW:
80 LoadImageRAW(filename, image);
81 break;
82 }
83 }
84
85 void ImageIO::LoadImageBMP(const char *filename, Image *image) {
86 FILE *fp = fopen(filename,"rb");
87 if(!fp) {
88 printf("Error opening %s!\n", filename);
89 return;
90 }
91
92 char header[2];
93 fread(header,1,2,fp);
94 if(!((header[0]=='B')&&(header[1]=='M'))) {
95 fclose(fp);
96 printf("Error loading image %s, wrong file format!\n",filename);
97 return;
98 }
99
100 long bmOffset;
101 fseek(fp,10,SEEK_SET);
102 fread(&bmOffset,4,1,fp);
103
104 fseek(fp,18,SEEK_SET);
105 fread(&(image->width),4,1,fp);
106 fread(&(image->height),4,1,fp);
107
108 short bpp;
109 fseek(fp,28,SEEK_SET);
110 fread(&bpp,2,1,fp);
111 if(!((bpp==8)||(bpp==24))) {
112 fclose(fp);
113 printf("Error loading image %s, can only load BMP files with 8 or 24 bpp!\n",filename);
114 return;
115 }
116
117 long compression;
118 fread(&compression,4,1,fp);
119 if(compression) {
120 fclose(fp);
121 printf("Error loading image %s, can only load uncompressed BMP files!\n",filename);
122 return;
123 }
124
125 if(image->data) free(image->data);
126 image->data = (unsigned char *)malloc(image->height * image->width * 3);
127
128 if(bpp == 8) {
129
130 //bytes per row
131 long bpr,tmp;
132 tmp = image->width % 4;
133 if(tmp == 0) {
134 bpr = image->width;
135 } else {
136 bpr = image->width + 4 - tmp;
137 tmp = 4 - tmp;
138 }
139
140
141 long bmSize = bpr * image->height;
142 unsigned char *buffer = (unsigned char *)malloc(bmSize);
143 fseek(fp,bmOffset,SEEK_SET);
144 fread(buffer,1,bmSize,fp);
145
146 long pos = 0;
147 for(long i=0;i<image->height;i++) {
148 for(long j=0;j<image->width;j++) {
149
150 image->SetPixelGray(j,image->height - i - 1,buffer[pos]);
151 pos++;
152 }
153 pos += tmp;
154 }
155
156 free(buffer);
157
158 } else if (bpp == 24) {
159
160 //bytes per row
161 long bpr,tmp;
162 tmp = (image->width*3) % 4;
163 if(tmp == 0) {
164 bpr = image->width * 3;
165 } else {
166 bpr = image->width * 3 + 4 - tmp;
167 tmp = 4 - tmp;
168 }
169
170 long bmSize = bpr * image->height;
171 unsigned char *buffer = (unsigned char *)malloc(bmSize);
172 fseek(fp,bmOffset,SEEK_SET);
173 fread(buffer,1,bmSize,fp);
174
175 long pos = 0;
176 Image::Pixel rgb;
177 for(long i=0;i<image->height;i++) {
178 for(long j=0;j<image->width;j++) {
179 rgb.B = buffer[pos++];
180 rgb.G = buffer[pos++];
181 rgb.R = buffer[pos++];
182 image->SetPixelColor(j,image->height - i - 1,rgb);
183 }
184 pos += tmp;
185 }
186
187 free(buffer);
188 }
189
190 fclose(fp);
191 }
192
193 void ImageIO::SaveImage(const char *filename, Image *image) {
194 int imgType = GetImageType(filename);
195 if(imgType == IMGTYPE_UNSUPPORTED) {
196 printf("Error saving image to %s, unknown image format!\n", filename);
197 return;
198 }
199 SaveImage(filename, image, imgType);
200 }
201
202 void ImageIO::SaveImage(const char *filename, Image *image, int imageType) {
203 switch(imageType) {
204 case IMGTYPE_BMP:
205 SaveImageBMP(filename, image);
206 break;
207 case IMGTYPE_PPM:
208 SaveImagePPM(filename, image);
209 break;
210 case IMGTYPE_PGM:
211 SaveImagePPM(filename, image);
212 break;
213 case IMGTYPE_RAW:
214 SaveImageRAW(filename, image);
215 break;
216 }
217 }
218
219 void ImageIO::SaveImageBMP(const char *filename, Image *image) {
220 FILE *fp = fopen(filename,"wb");
221 if(!fp) {
222 printf("Error opening %s!\n", filename);
223 return;
224 }
225
226 char header[2];
227 long tmpl;
228 short tmps;
229
230 //header
231 header[0] = 'B';
232 header[1] = 'M';
233 fwrite(header,2,1,fp);
234
235 //filesize;
236 long rowsize;
237 long tmp = (image->width*3)%4;
238 if(tmp==0) rowsize = image->width*3;
239 else rowsize = image->width*3 + 4 - tmp;
240 unsigned char *row = (unsigned char *)malloc(rowsize);
241 tmpl = 54 + rowsize*image->height;
242 fwrite(&tmpl,4,1,fp);
243
244 tmps = 0;
245 fwrite(&tmps,2,1,fp);
246 fwrite(&tmps,2,1,fp);
247
248 //offset to the beginning of bm data
249 tmpl = 54;
250 fwrite(&tmpl,4,1,fp);
251
252 //info header size
253 tmpl = 40;
254 fwrite(&tmpl,4,1,fp);
255
256 //size
257 tmpl = image->width;
258 fwrite(&tmpl,4,1,fp);
259 tmpl = image->height;
260 fwrite(&tmpl,4,1,fp);
261
262 tmps = 1;
263 fwrite(&tmps,2,1,fp);
264 tmps = 24; //bpp
265 fwrite(&tmps,2,1,fp);
266 tmpl = 0;
267 fwrite(&tmpl,4,1,fp);
268 fwrite(&tmpl,4,1,fp);
269 fwrite(&tmpl,4,1,fp);
270 fwrite(&tmpl,4,1,fp);
271 fwrite(&tmpl,4,1,fp);
272 fwrite(&tmpl,4,1,fp);
273
274 //actual bitmap data
275 for(long i = 0; i<image->height;i++) {
276 memset(row,0,rowsize);
277 memcpy(row,image->data + (3*image->width)*(image->height-i-1),3*image->width);
278 fwrite(row,rowsize,1,fp);
279 }
280
281 free(row);
282
283 fclose(fp);
284 }
285
286 void ImageIO::LoadImagePPM(const char *filename, Image *image) {
287 FILE *fp = fopen(filename,"rb");
288 if(!fp) {
289 printf("Error opening %s!\n", filename);
290 return;
291 }
292
293 long filesize;
294 fseek(fp,0,SEEK_END);
295 filesize = ftell(fp);
296 fseek(fp,0,SEEK_SET);
297
298 unsigned char *buffer = (unsigned char *)malloc(filesize);
299 fread(buffer,1,filesize,fp);
300
301 char id[1024];
302 long sizex, sizey, levels;
303 sscanf((char *)buffer,"%s\n%ld %ld\n%ld\n",id,&sizex,&sizey,&levels);
304
305 if((strncmp(id,"P6",2)!=0)||(levels!=255)) {
306 free(buffer);
307 fclose(fp);
308 printf("Error loading image %s, wrong file format!\n",filename);
309 return;
310 }
311
312 image->width = sizex;
313 image->height = sizey;
314
315 if(image->data) free(image->data);
316 image->data = (unsigned char *)malloc(image->height * image->width * 3);
317
318 long pos = filesize - sizex*sizey*3;
319 for(long i = 0; i < sizey;i++) {
320 for(long j = 0; j < sizex;j++) {
321 Image::Pixel rgb;
322 rgb.R = buffer[pos++];
323 rgb.G = buffer[pos++];
324 rgb.B = buffer[pos++];
325 image->SetPixelColor(j,i,rgb);
326 }
327 }
328
329 free(buffer);
330
331 fclose(fp);
332 }
333
334 void ImageIO::LoadImagePGM(const char *filename, Image *image) {
335 FILE *fp = fopen(filename,"rb");
336 if(!fp) {
337 printf("Error opening %s!\n", filename);
338 return;
339 }
340
341 long filesize;
342 fseek(fp,0,SEEK_END);
343 filesize = ftell(fp);
344 fseek(fp,0,SEEK_SET);
345
346 unsigned char *buffer = (unsigned char *)malloc(filesize);
347 fread(buffer,1,filesize,fp);
348
349 char id[1024];
350 long sizex, sizey, levels;
351 sscanf((char *)buffer,"%s\n%ld %ld\n%ld\n",id,&sizex,&sizey,&levels);
352
353 if((strncmp(id,"P5",2)!=0)||(levels!=255)) {
354 free(buffer);
355 fclose(fp);
356 printf("Error loading image %s, wrong file format!\n",filename);
357 return;
358 }
359
360 image->width = sizex;
361 image->height = sizey;
362
363 if(image->data) free(image->data);
364 image->data = (unsigned char *)malloc(image->height * image->width * 3);
365
366 long pos = filesize - sizex*sizey;
367 for(long i = 0; i < sizey;i++) {
368 for(long j = 0; j < sizex;j++) {
369 image->SetPixelGray(j,i,buffer[pos]);
370 pos++;
371 }
372 }
373
374 free(buffer);
375
376 fclose(fp);
377 }
378
379 void ImageIO::SaveImagePPM(const char *filename, Image *image) {
380 FILE *fp = fopen(filename,"wb");
381 if(!fp) {
382 printf("Error opening %s!\n", filename);
383 return;
384 }
385
386 fprintf(fp,"P6\n%ld %ld\n255\n",image->width,image->height);
387
388 long sizex = image->width;
389 long sizey = image->height;
390 unsigned char *buffer = (unsigned char *)malloc(image->width * image->height * 3);
391 long pos = 0;
392 for(long i = 0; i < sizey;i++) {
393 for(long j = 0; j < sizex;j++) {
394 Image::Pixel rgb = image->GetPixelColor(j,i);
395 buffer[pos++] = rgb.R;
396 buffer[pos++] = rgb.G;
397 buffer[pos++] = rgb.B;
398 }
399 }
400
401 fwrite(buffer,1,image->width * image->height * 3,fp);
402
403 free(buffer);
404 fclose(fp);
405 }
406
407 void ImageIO::SaveImagePGM(const char *filename, Image *image) {
408 FILE *fp = fopen(filename,"wb");
409 if(!fp) {
410 printf("Error opening %s!\n", filename);
411 return;
412 }
413
414 fprintf(fp,"P5\n%ld %ld\n255\n",image->width,image->height);
415
416 long sizex = image->width;
417 long sizey = image->height;
418 unsigned char *buffer = (unsigned char *)malloc(image->width * image->height);
419 long pos = 0;
420 for(long i = 0; i < sizey;i++) {
421 for(long j = 0; j < sizex;j++) {
422 buffer[pos++] = image->GetPixelGray(j,i);
423 }
424 }
425
426 fwrite(buffer,1,image->width * image->height,fp);
427
428 free(buffer);
429 fclose(fp);
430 }
431
432 void ImageIO::LoadImageRAW(const char *filename, Image *image, long width, long height) {
433 FILE *fp = fopen(filename,"rb");
434 if(!fp) {
435 printf("Error opening %s!\n", filename);
436 return;
437 }
438
439 if((width==0)||(height==0)) {
440 long filesize;
441 fseek(fp,0,SEEK_END);
442 filesize = ftell(fp);
443 fseek(fp,0,SEEK_SET);
444 width = (long)sqrt((double)filesize);
445 height = width;
446 if((height*width)!=filesize) {
447 fclose(fp);
448 printf("Error loading image %s, wrong file format!\n",filename);
449 return;
450 }
451 }
452
453 image->width = width;
454 image->height = height;
455 if(image->data) free(image->data);
456 image->data = (unsigned char *)malloc(image->height * image->width * 3);
457
458 unsigned char *buffer = (unsigned char *)malloc(image->width * image->height);
459 fread(buffer,1,image->width * image->height,fp);
460
461 long pos = 0;
462 for(long i = 0; i < height;i++) {
463 for(long j = 0; j < width;j++) {
464 unsigned char c = buffer[pos++];
465 image->SetPixelGray(j,i,c);
466 }
467 }
468
469 free(buffer);
470 fclose(fp);
471 }
472
473 void ImageIO::SaveImageRAW(const char *filename, Image *image) {
474 FILE *fp = fopen(filename,"wb");
475 if(!fp) {
476 printf("Error opening %s!\n", filename);
477 return;
478 }
479
480 long sizex = image->width;
481 long sizey = image->height;
482 unsigned char *buffer = (unsigned char *)malloc(image->width * image->height);
483
484 long pos = 0;
485 for(long i = 0; i < sizey;i++) {
486 for(long j = 0; j < sizex;j++) {
487 unsigned char c = image->GetPixelGray(j,i);
488 buffer[pos++] = c;
489 }
490 }
491
492 fwrite(buffer,1,image->width * image->height,fp);
493
494 free(buffer);
495 fclose(fp);
496 }
Show file before | Show file after | Hide comments
@@ -0,0 +1,81
1 //Copyright (C) 2011 by Ivan Fratric
2 //
3 //Permission is hereby granted, free of charge, to any person obtaining a copy
4 //of this software and associated documentation files (the "Software"), to deal
5 //in the Software without restriction, including without limitation the rights
6 //to use, copy, modify, merge, publish, distribute, sublicense, and/or sell
7 //copies of the Software, and to permit persons to whom the Software is
8 //furnished to do so, subject to the following conditions:
9 //
10 //The above copyright notice and this permission notice shall be included in
11 //all copies or substantial portions of the Software.
12 //
13 //THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
14 //IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
15 //FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
16 //AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
17 //LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
18 //OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN
19 //THE SOFTWARE.
20
21
22 #pragma once
23
24 #define IMGTYPE_RAW 0
25 #define IMGTYPE_BMP 1
26 #define IMGTYPE_PPM 2
27 #define IMGTYPE_PGM 3
28 #define IMGTYPE_UNSUPPORTED 999
29
30 //handles basic image file input/output
31 //only supports uncompressed image formats
32 class ImageIO
33 {
34 protected:
35 //gets the file extension of file filename
36 const char *GetFileExtension(const char *filename);
37
38 //determines the imege format from the filename
39 int GetImageType(const char *filename);
40
41 public:
42
43 //loads the image from filename into image
44 //automatically determines the image format
45 void LoadImage(const char *filename, Image *image);
46
47 //loads the image of the specified format (imageType) from filename into image
48 void LoadImage(const char *filename, Image *image, int imageType);
49
50 //saves the image into file named 'filename'
51 //automatically determines the image format
52 void SaveImage(const char *filename, Image *image);
53
54 //saves the image into file named 'filename', using the format given as imageType
55 void SaveImage(const char *filename, Image *image, int imageType);
56
57 //loads the uncompressed BMP image from filename into image
58 void LoadImageBMP(const char *filename, Image *image);
59 //saves the image into file named 'filename' in uncompressed BMP format
60 void SaveImageBMP(const char *filename, Image *image);
61
62 //loads the PPM image from filename into image
63 void LoadImagePPM(const char *filename, Image *image);
64 //saves the image into file named 'filename' in PPM format
65 void SaveImagePPM(const char *filename, Image *image);
66
67 //loads the PGM image from filename into image
68 void LoadImagePGM(const char *filename, Image *image);
69 //saves the image into file named 'filename' in PGM format
70 void SaveImagePGM(const char *filename, Image *image);
71
72 //loads the image from the file named 'filename'
73 //the file is assumed to be structured so that it only contains an array of raw (gray) pixel values
74 //as the file does not contain the image width and height, those are passed as parameters to the function
75 //if width and height are 0, the image is assumed to be square and the width and height are computed based on the file size
76 void LoadImageRAW(const char *filename, Image *image, long width = 0, long height = 0);
77
78 //saves the image to a file named 'filename'
79 //only the array of raw (gray) pixel values is stored, without additional information such as image size
80 void SaveImageRAW(const char *filename, Image *image);
81 };
Show file before | Show file after | Hide comments
@@ -0,0 +1,360
1 //Copyright (C) 2011 by Ivan Fratric
2 //
3 //Permission is hereby granted, free of charge, to any person obtaining a copy
4 //of this software and associated documentation files (the "Software"), to deal
5 //in the Software without restriction, including without limitation the rights
6 //to use, copy, modify, merge, publish, distribute, sublicense, and/or sell
7 //copies of the Software, and to permit persons to whom the Software is
8 //furnished to do so, subject to the following conditions:
9 //
10 //The above copyright notice and this permission notice shall be included in
11 //all copies or substantial portions of the Software.
12 //
13 //THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
14 //IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
15 //FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
16 //AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
17 //LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
18 //OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN
19 //THE SOFTWARE.
20
21 #define _CRT_SECURE_NO_WARNINGS
22
23 #include <stdio.h>
24 #include <list>
25 #include <limits>
26
27 using namespace std;
28
29 #include "polypartition.h"
30
31 #include "image.h"
32 #include "imageio.h"
33
34 void ReadPoly(FILE *fp, TPPLPoly *poly) {
35 int i,numpoints,hole;
36 float x,y;
37
38 fscanf(fp,"%d\n",&numpoints);
39 poly->Init(numpoints);
40
41 fscanf(fp,"%d\n",&hole);
42 if(hole) poly->SetHole(true);
43
44 for(i=0;i<numpoints;i++) {
45 fscanf(fp,"%g %g\n",&x, &y);
46 (*poly)[i].x = x;
47 (*poly)[i].y = y;
48 }
49 }
50
51 void ReadPoly(const char *filename, TPPLPoly *poly) {
52 FILE *fp = fopen(filename,"r");
53 if(!fp) {
54 printf("Error reading file %s\n", filename);
55 return;
56 }
57 ReadPoly(fp,poly);
58 fclose(fp);
59 }
60
61 void ReadPolyList(FILE *fp, list<TPPLPoly> *polys) {
62 int i,numpolys;
63 TPPLPoly poly;
64
65 polys->clear();
66 fscanf(fp,"%d\n",&numpolys);
67 for(i=0;i<numpolys;i++) {
68 ReadPoly(fp,&poly);
69 polys->push_back(poly);
70 }
71 }
72
73 void ReadPolyList(const char *filename, list<TPPLPoly> *polys) {
74 FILE *fp = fopen(filename,"r");
75 if(!fp) {
76 printf("Error reading file %s\n", filename);
77 return;
78 }
79 ReadPolyList(fp,polys);
80 fclose(fp);
81 }
82
83
84 void WritePoly(FILE *fp, TPPLPoly *poly) {
85 int i,numpoints;
86 numpoints = poly->GetNumPoints();
87
88 fprintf(fp,"%d\n",numpoints);
89
90 if(poly->IsHole()) {
91 fprintf(fp,"1\n");
92 } else {
93 fprintf(fp,"0\n");
94 }
95
96 for(i=0;i<numpoints;i++) {
97 fprintf(fp,"%g %g\n",(*poly)[i].x, (*poly)[i].y);
98 }
99 }
100
101 void WritePoly(const char *filename, TPPLPoly *poly) {
102 FILE *fp = fopen(filename,"w");
103 if(!fp) {
104 printf("Error writing file %s\n", filename);
105 return;
106 }
107 WritePoly(fp,poly);
108 fclose(fp);
109 }
110
111 void WritePolyList(FILE *fp, list<TPPLPoly> *polys) {
112 list<TPPLPoly>::iterator iter;
113
114 fprintf(fp,"%ld\n",polys->size());
115
116 for(iter = polys->begin(); iter != polys->end(); iter++) {
117 WritePoly(fp,&(*iter));
118 }
119 }
120
121 void WritePolyList(const char *filename, list<TPPLPoly> *polys) {
122 FILE *fp = fopen(filename,"w");
123 if(!fp) {
124 printf("Error writing file %s\n", filename);
125 return;
126 }
127 WritePolyList(fp,polys);
128 fclose(fp);
129 }
130
131 void DrawPoly(Image *img, TPPLPoly *poly, tppl_float xmin, tppl_float xmax, tppl_float ymin, tppl_float ymax) {
132 TPPLPoint p1,p2,p1img,p2img,polymin,imgmin;
133 long i;
134 Image::Pixel color={0,0,0};
135
136 polymin.x = xmin;
137 polymin.y = ymin;
138 imgmin.x = 5;
139 imgmin.y = 5;
140
141 tppl_float polySizeX = xmax - xmin;
142 tppl_float polySizeY = ymax - ymin;
143 tppl_float imgSizeX = (tppl_float)img->GetWidth()-10;
144 tppl_float imgSizeY = (tppl_float)img->GetHeight()-10;
145
146 tppl_float scalex = 0;
147 tppl_float scaley = 0;
148 tppl_float scale;
149 if(polySizeX>0) scalex = imgSizeX/polySizeX;
150 if(polySizeY>0) scaley = imgSizeY/polySizeY;
151
152 if(scalex>0 && scalex<scaley) scale = scalex;
153 else if(scaley>0) scale = scaley;
154 else scale = 1;
155
156 for(i=0;i<poly->GetNumPoints();i++) {
157 p1 = poly->GetPoint(i);
158 p2 = poly->GetPoint((i+1)%poly->GetNumPoints());
159 p1img = (p1 - polymin)*scale + imgmin;
160 p2img = (p2 - polymin)*scale + imgmin;
161 img->DrawLine((int)p1img.x,(int)p1img.y,(int)p2img.x,(int)p2img.y,color);
162 }
163 }
164
165 void DrawPoly(const char *filename, TPPLPoly *poly) {
166 Image img(500,500);
167 Image::Pixel white={255,255,255};
168 img.Clear(white);
169 ImageIO io;
170
171 tppl_float xmin = std::numeric_limits<tppl_float>::max();
172 tppl_float xmax = std::numeric_limits<tppl_float>::min();
173 tppl_float ymin = std::numeric_limits<tppl_float>::max();
174 tppl_float ymax = std::numeric_limits<tppl_float>::min();
175 for(int i=0;i<poly->GetNumPoints();i++) {
176 if(poly->GetPoint(i).x < xmin) xmin = poly->GetPoint(i).x;
177 if(poly->GetPoint(i).x > xmax) xmax = poly->GetPoint(i).x;
178 if(poly->GetPoint(i).y < ymin) ymin = poly->GetPoint(i).y;
179 if(poly->GetPoint(i).y > ymax) ymax = poly->GetPoint(i).y;
180 }
181
182 DrawPoly(&img, poly, xmin, xmax, ymin, ymax);
183
184 io.SaveImage(filename,&img);
185 }
186
187 void DrawPolyList(const char *filename, list<TPPLPoly> *polys) {
188 Image img(500,500);
189 Image::Pixel white={255,255,255};
190 img.Clear(white);
191
192 ImageIO io;
193 list<TPPLPoly>::iterator iter;
194
195 tppl_float xmin = std::numeric_limits<tppl_float>::max();
196 tppl_float xmax = std::numeric_limits<tppl_float>::min();
197 tppl_float ymin = std::numeric_limits<tppl_float>::max();
198 tppl_float ymax = std::numeric_limits<tppl_float>::min();
199 for(iter=polys->begin(); iter!=polys->end(); iter++) {
200 for(int i=0;i<iter->GetNumPoints();i++) {
201 if(iter->GetPoint(i).x < xmin) xmin = iter->GetPoint(i).x;
202 if(iter->GetPoint(i).x > xmax) xmax = iter->GetPoint(i).x;
203 if(iter->GetPoint(i).y < ymin) ymin = iter->GetPoint(i).y;
204 if(iter->GetPoint(i).y > ymax) ymax = iter->GetPoint(i).y;
205 }
206 //if(iter->GetOrientation() == TPPL_CCW) printf("CCW\n");
207 //else if (iter->GetOrientation() == TPPL_CW) printf("CW\n");
208 //else printf("gfdgdg\n");
209 }
210 //printf("\n");
211
212 for(iter=polys->begin(); iter!=polys->end(); iter++) {
213 DrawPoly(&img, &(*iter), xmin, xmax, ymin, ymax);
214 }
215
216 io.SaveImage(filename,&img);
217 }
218
219 bool ComparePoly(TPPLPoly *p1, TPPLPoly *p2) {
220 long i,n = p1->GetNumPoints();
221 if(n!=p2->GetNumPoints()) return false;
222 for(i=0;i<n;i++) {
223 if((*p1)[i]!=(*p2)[i]) return false;
224 }
225 return true;
226 }
227
228 bool ComparePoly(list<TPPLPoly> *polys1, list<TPPLPoly> *polys2) {
229 list<TPPLPoly>::iterator iter1, iter2;
230 long i,n = (long)polys1->size();
231 if(n!=(signed)polys2->size()) return false;
232 iter1 = polys1->begin();
233 iter2 = polys2->begin();
234 for(i=0;i<n;i++) {
235 if(!ComparePoly(&(*iter1),&(*iter2))) return false;
236 iter1++;
237 iter2++;
238 }
239 return true;
240 }
241
242
243 void GenerateTestData() {
244 TPPLPartition pp;
245
246 list<TPPLPoly> testpolys,result,expectedResult;
247
248 ReadPolyList("test_input.txt",&testpolys);
249
250 DrawPolyList("test_input.bmp",&testpolys);
251
252 pp.Triangulate_EC(&testpolys,&result);
253 //pp.Triangulate_EC(&(*testpolys.begin()),&result);
254 DrawPolyList("test_triangulate_EC.bmp",&result);
255 WritePolyList("test_triangulate_EC.txt",&result);
256
257 result.clear(); expectedResult.clear();
258
259 pp.Triangulate_OPT(&(*testpolys.begin()),&result);
260 DrawPolyList("test_triangulate_OPT.bmp",&result);
261 WritePolyList("test_triangulate_OPT.txt",&result);
262
263 result.clear(); expectedResult.clear();
264
265 pp.Triangulate_MONO(&testpolys,&result);
266 //pp.Triangulate_MONO(&(*testpolys.begin()),&result);
267 DrawPolyList("test_triangulate_MONO.bmp",&result);
268 WritePolyList("test_triangulate_MONO.txt",&result);
269
270 result.clear(); expectedResult.clear();
271
272 pp.ConvexPartition_HM(&testpolys,&result);
273 //pp.ConvexPartition_HM(&(*testpolys.begin()),&result);
274 DrawPolyList("test_convexpartition_HM.bmp",&result);
275 WritePolyList("test_convexpartition_HM.txt",&result);
276
277 result.clear(); expectedResult.clear();
278
279 pp.ConvexPartition_OPT(&(*testpolys.begin()),&result);
280 DrawPolyList("test_convexpartition_OPT.bmp",&result);
281 WritePolyList("test_convexpartition_OPT.txt",&result);
282 }
283
284 int main() {
285 TPPLPartition pp;
286 list<TPPLPoly> testpolys,result;
287
288 ReadPolyList("failing_mono_clean - copy.txt",&testpolys);
289 DrawPolyList("test.bmp", &testpolys);
290 if(!pp.Triangulate_MONO(&testpolys,&result)) printf("Error\n");
291 DrawPolyList("test2.bmp", &result);
292
293 }
294
295 /*int main()
296 {
297 TPPLPartition pp;
298
299 list<TPPLPoly> testpolys,result,expectedResult;
300
301 ReadPolyList("test_input.txt",&testpolys);
302
303 DrawPolyList("test_input.bmp",&testpolys);
304
305 printf("Testing Triangulate_EC : ");
306 pp.Triangulate_EC(&testpolys,&result);
307 ReadPolyList("test_triangulate_EC.txt",&expectedResult);
308 if(ComparePoly(&result,&expectedResult)) {
309 printf("success\n");
310 } else {
311 printf("failed\n");
312 }
313
314 result.clear(); expectedResult.clear();
315
316 printf("Testing Triangulate_OPT : ");
317 pp.Triangulate_OPT(&(*testpolys.begin()),&result);
318 ReadPolyList("test_triangulate_OPT.txt",&expectedResult);
319 if(ComparePoly(&result,&expectedResult)) {
320 printf("success\n");
321 } else {
322 printf("failed\n");
323 }
324
325 result.clear(); expectedResult.clear();
326
327 printf("Testing Triangulate_MONO : ");
328 pp.Triangulate_MONO(&testpolys,&result);
329 ReadPolyList("test_triangulate_MONO.txt",&expectedResult);
330 if(ComparePoly(&result,&expectedResult)) {
331 printf("success\n");
332 } else {
333 printf("failed\n");
334 }
335
336 result.clear(); expectedResult.clear();
337
338 printf("Testing ConvexPartition_HM : ");
339 pp.ConvexPartition_HM(&testpolys,&result);
340 ReadPolyList("test_convexpartition_HM.txt",&expectedResult);
341 if(ComparePoly(&result,&expectedResult)) {
342 printf("success\n");
343 } else {
344 printf("failed\n");
345 }
346
347 result.clear(); expectedResult.clear();
348
349 printf("Testing ConvexPartition_OPT : ");
350 pp.ConvexPartition_OPT(&(*testpolys.begin()),&result);
351 ReadPolyList("test_convexpartition_OPT.txt",&expectedResult);
352 if(ComparePoly(&result,&expectedResult)) {
353 printf("success\n");
354 } else {
355 printf("failed\n");
356 }
357
358 return 0;
359 }*/
360
Show file before | Show file after | Hide comments
@@ -0,0 +1,135
1 21
2 3
3 0
4 179 196
5 189 172
6 189 242
7 3
8 0
9 125 191
10 153 197
11 132 221
12 5
13 0
14 150 266
15 132 221
16 179 196
17 189 242
18 196 310
19 5
20 0
21 230 99
22 230 80
23 254 79
24 254 98
25 235 163
26 4
27 0
28 212 144
29 230 99
30 235 163
31 212 173
32 6
33 0
34 163 138
35 212 144
36 212 173
37 189 172
38 159 161
39 141 138
40 5
41 0
42 50 98
43 50 79
44 74 80
45 74 99
46 69 163
47 4
48 0
49 69 163
50 74 99
51 92 144
52 92 173
53 5
54 0
55 115 172
56 92 173
57 92 144
58 141 138
59 159 161
60 4
61 0
62 189 172
63 179 196
64 150 183
65 159 161
66 4
67 0
68 253 377
69 208 377
70 208 355
71 228 358
72 4
73 0
74 96 355
75 96 377
76 51 377
77 76 358
78 3
79 0
80 228 358
81 254 361
82 253 377
83 5
84 0
85 219 301
86 228 358
87 208 355
88 196 310
89 189 242
90 3
91 0
92 51 377
93 50 361
94 76 358
95 5
96 0
97 108 310
98 96 355
99 76 358
100 85 301
101 115 242
102 4
103 0
104 150 266
105 108 310
106 115 242
107 132 221
108 4
109 0
110 132 221
111 115 242
112 115 172
113 125 191
114 3
115 0
116 159 161
117 125 191
118 115 172
119 4
120 0
121 163 125
122 163 138
123 141 138
124 141 125
125 9
126 0
127 152 71
128 170 75
129 179 87
130 178 108
131 163 125
132 141 125
133 126 108
134 125 87
135 134 75
Show file before | Show file after | Hide comments
@@ -0,0 +1,111
1 17
2 9
3 0
4 170 75
5 179 87
6 178 108
7 163 125
8 141 125
9 126 108
10 125 87
11 134 75
12 152 71
13 4
14 0
15 163 125
16 163 138
17 141 138
18 141 125
19 5
20 0
21 163 138
22 212 144
23 212 173
24 189 172
25 141 138
26 6
27 0
28 189 172
29 189 242
30 150 266
31 115 242
32 115 172
33 141 138
34 4
35 0
36 212 144
37 230 99
38 235 163
39 212 173
40 4
41 0
42 115 172
43 92 173
44 92 144
45 141 138
46 3
47 0
48 150 266
49 108 310
50 115 242
51 3
52 0
53 189 242
54 196 310
55 150 266
56 5
57 0
58 230 99
59 230 80
60 254 79
61 254 98
62 235 163
63 4
64 0
65 92 173
66 69 163
67 74 99
68 92 144
69 4
70 0
71 108 310
72 96 355
73 85 301
74 115 242
75 4
76 0
77 189 242
78 219 301
79 208 355
80 196 310
81 5
82 0
83 69 163
84 50 98
85 50 79
86 74 80
87 74 99
88 4
89 0
90 96 355
91 96 377
92 76 358
93 85 301
94 4
95 0
96 219 301
97 228 358
98 208 377
99 208 355
100 4
101 0
102 96 377
103 51 377
104 50 361
105 76 358
106 4
107 0
108 228 358
109 254 361
110 253 377
111 208 377
Show file before | Show file after | Hide comments
@@ -0,0 +1,55
1 2
2 44
3 0
4 170 75
5 179 87
6 178 108
7 163 125
8 163 138
9 212 144
10 230 99
11 230 80
12 254 79
13 254 98
14 235 163
15 212 173
16 189 172
17 189 242
18 219 301
19 228 358
20 254 361
21 253 377
22 208 377
23 208 355
24 196 310
25 150 266
26 108 310
27 96 355
28 96 377
29 51 377
30 50 361
31 76 358
32 85 301
33 115 242
34 115 172
35 92 173
36 69 163
37 50 98
38 50 79
39 74 80
40 74 99
41 92 144
42 141 138
43 141 125
44 126 108
45 125 87
46 134 75
47 152 71
48 6
49 1
50 159 161
51 125 191
52 153 197
53 132 221
54 179 196
55 150 183
Show file before | Show file after | Hide comments
@@ -0,0 +1,251
1 50
2 3
3 0
4 179 196
5 189 172
6 189 242
7 3
8 0
9 125 191
10 153 197
11 132 221
12 3
13 0
14 132 221
15 179 196
16 189 242
17 3
18 0
19 230 80
20 254 79
21 254 98
22 3
23 0
24 230 99
25 230 80
26 254 98
27 3
28 0
29 230 99
30 254 98
31 235 163
32 3
33 0
34 212 144
35 230 99
36 235 163
37 3
38 0
39 212 144
40 235 163
41 212 173
42 3
43 0
44 212 144
45 212 173
46 189 172
47 3
48 0
49 163 138
50 212 144
51 189 172
52 3
53 0
54 50 98
55 50 79
56 74 80
57 3
58 0
59 50 98
60 74 80
61 74 99
62 3
63 0
64 69 163
65 50 98
66 74 99
67 3
68 0
69 69 163
70 74 99
71 92 144
72 3
73 0
74 92 173
75 69 163
76 92 144
77 3
78 0
79 115 172
80 92 173
81 92 144
82 3
83 0
84 115 172
85 92 144
86 141 138
87 3
88 0
89 189 172
90 179 196
91 150 183
92 3
93 0
94 189 172
95 150 183
96 159 161
97 3
98 0
99 163 138
100 189 172
101 159 161
102 3
103 0
104 253 377
105 208 377
106 208 355
107 3
108 0
109 96 355
110 96 377
111 51 377
112 3
113 0
114 228 358
115 254 361
116 253 377
117 3
118 0
119 228 358
120 253 377
121 208 355
122 3
123 0
124 219 301
125 228 358
126 208 355
127 3
128 0
129 219 301
130 208 355
131 196 310
132 3
133 0
134 189 242
135 219 301
136 196 310
137 3
138 0
139 189 242
140 196 310
141 150 266
142 3
143 0
144 132 221
145 189 242
146 150 266
147 3
148 0
149 51 377
150 50 361
151 76 358
152 3
153 0
154 96 355
155 51 377
156 76 358
157 3
158 0
159 96 355
160 76 358
161 85 301
162 3
163 0
164 108 310
165 96 355
166 85 301
167 3
168 0
169 108 310
170 85 301
171 115 242
172 3
173 0
174 150 266
175 108 310
176 115 242
177 3
178 0
179 132 221
180 150 266
181 115 242
182 3
183 0
184 132 221
185 115 242
186 115 172
187 3
188 0
189 125 191
190 132 221
191 115 172
192 3
193 0
194 159 161
195 125 191
196 115 172
197 3
198 0
199 159 161
200 115 172
201 141 138
202 3
203 0
204 163 138
205 159 161
206 141 138
207 3
208 0
209 163 125
210 163 138
211 141 138
212 3
213 0
214 163 125
215 141 138
216 141 125
217 3
218 0
219 178 108
220 163 125
221 141 125
222 3
223 0
224 178 108
225 141 125
226 126 108
227 3
228 0
229 179 87
230 178 108
231 126 108
232 3
233 0
234 179 87
235 126 108
236 125 87
237 3
238 0
239 170 75
240 179 87
241 125 87
242 3
243 0
244 152 71
245 170 75
246 125 87
247 3
248 0
249 152 71
250 125 87
251 134 75
Show file before | Show file after | Hide comments
@@ -0,0 +1,261
1 52
2 3
3 0
4 212 144
5 92 144
6 163 138
7 3
8 0
9 163 138
10 92 144
11 141 138
12 3
13 0
14 163 138
15 141 138
16 163 125
17 3
18 0
19 163 125
20 141 138
21 141 125
22 3
23 0
24 163 125
25 141 125
26 178 108
27 3
28 0
29 178 108
30 141 125
31 126 108
32 3
33 0
34 178 108
35 126 108
36 179 87
37 3
38 0
39 179 87
40 126 108
41 125 87
42 3
43 0
44 179 87
45 125 87
46 170 75
47 3
48 0
49 170 75
50 125 87
51 134 75
52 3
53 0
54 170 75
55 134 75
56 152 71
57 3
58 0
59 50 361
60 96 377
61 51 377
62 3
63 0
64 76 358
65 96 377
66 50 361
67 3
68 0
69 96 377
70 76 358
71 96 355
72 3
73 0
74 108 310
75 96 355
76 76 358
77 3
78 0
79 108 310
80 76 358
81 85 301
82 3
83 0
84 108 310
85 85 301
86 150 266
87 3
88 0
89 189 242
90 150 266
91 85 301
92 3
93 0
94 189 242
95 85 301
96 115 242
97 3
98 0
99 132 221
100 189 242
101 115 242
102 3
103 0
104 179 196
105 189 242
106 132 221
107 3
108 0
109 189 242
110 179 196
111 189 172
112 3
113 0
114 179 196
115 150 183
116 189 172
117 3
118 0
119 189 172
120 150 183
121 159 161
122 3
123 0
124 235 163
125 189 172
126 159 161
127 3
128 0
129 212 144
130 235 163
131 159 161
132 3
133 0
134 230 99
135 235 163
136 212 144
137 3
138 0
139 235 163
140 230 99
141 254 98
142 3
143 0
144 254 98
145 230 99
146 230 80
147 3
148 0
149 254 98
150 230 80
151 254 79
152 3
153 0
154 212 173
155 189 172
156 235 163
157 3
158 0
159 212 173
160 189 172
161 235 163
162 3
163 0
164 253 377
165 208 377
166 254 361
167 3
168 0
169 228 358
170 254 361
171 208 377
172 3
173 0
174 228 358
175 208 377
176 208 355
177 3
178 0
179 196 310
180 228 358
181 208 355
182 3
183 0
184 228 358
185 196 310
186 219 301
187 3
188 0
189 219 301
190 196 310
191 150 266
192 3
193 0
194 219 301
195 150 266
196 189 242
197 3
198 0
199 125 191
200 153 197
201 132 221
202 3
203 0
204 125 191
205 132 221
206 115 242
207 3
208 0
209 125 191
210 115 242
211 115 172
212 3
213 0
214 125 191
215 115 172
216 159 161
217 3
218 0
219 115 172
220 69 163
221 159 161
222 3
223 0
224 212 144
225 159 161
226 69 163
227 3
228 0
229 92 144
230 212 144
231 69 163
232 3
233 0
234 74 99
235 92 144
236 69 163
237 3
238 0
239 74 99
240 69 163
241 50 98
242 3
243 0
244 74 99
245 50 98
246 74 80
247 3
248 0
249 74 80
250 50 98
251 50 79
252 3
253 0
254 92 173
255 69 163
256 115 172
257 3
258 0
259 115 172
260 92 173
261 69 163
Show file before | Show file after | Hide comments
@@ -0,0 +1,211
1 42
2 3
3 0
4 170 75
5 179 87
6 152 71
7 3
8 0
9 179 87
10 178 108
11 152 71
12 3
13 0
14 178 108
15 141 125
16 152 71
17 3
18 0
19 178 108
20 163 125
21 141 125
22 3
23 0
24 141 125
25 125 87
26 152 71
27 3
28 0
29 163 125
30 163 138
31 141 125
32 3
33 0
34 141 125
35 126 108
36 125 87
37 3
38 0
39 125 87
40 134 75
41 152 71
42 3
43 0
44 163 138
45 141 138
46 141 125
47 3
48 0
49 163 138
50 189 172
51 141 138
52 3
53 0
54 163 138
55 212 144
56 189 172
57 3
58 0
59 189 172
60 115 172
61 141 138
62 3
63 0
64 212 144
65 212 173
66 189 172
67 3
68 0
69 189 172
70 189 242
71 115 172
72 3
73 0
74 115 172
75 92 144
76 141 138
77 3
78 0
79 212 144
80 235 163
81 212 173
82 3
83 0
84 189 242
85 115 242
86 115 172
87 3
88 0
89 115 172
90 92 173
91 92 144
92 3
93 0
94 212 144
95 254 98
96 235 163
97 3
98 0
99 189 242
100 150 266
101 115 242
102 3
103 0
104 92 173
105 69 163
106 92 144
107 3
108 0
109 212 144
110 230 99
111 254 98
112 3
113 0
114 189 242
115 196 310
116 150 266
117 3
118 0
119 150 266
120 108 310
121 115 242
122 3
123 0
124 69 163
125 50 98
126 92 144
127 3
128 0
129 230 99
130 230 80
131 254 98
132 3
133 0
134 189 242
135 219 301
136 196 310
137 3
138 0
139 108 310
140 85 301
141 115 242
142 3
143 0
144 50 98
145 74 99
146 92 144
147 3
148 0
149 230 80
150 254 79
151 254 98
152 3
153 0
154 219 301
155 208 355
156 196 310
157 3
158 0
159 108 310
160 96 355
161 85 301
162 3
163 0
164 50 98
165 74 80
166 74 99
167 3
168 0
169 219 301
170 228 358
171 208 355
172 3
173 0
174 96 355
175 76 358
176 85 301
177 3
178 0
179 50 98
180 50 79
181 74 80
182 3
183 0
184 228 358
185 208 377
186 208 355
187 3
188 0
189 96 355
190 96 377
191 76 358
192 3
193 0
194 228 358
195 253 377
196 208 377
197 3
198 0
199 96 377
200 51 377
201 76 358
202 3
203 0
204 228 358
205 254 361
206 253 377
207 3
208 0
209 51 377
210 50 361
211 76 358
Show file before | Show file after | Hide comments
@@ -30,7 +30,8 SOURCES += main.cpp\
30 30 pcbcontext.cpp \
31 31 pcbvia.cpp \
32 32 pcbpad.cpp \
33 pcbzone.cpp
33 pcbzone.cpp \
34 polypartition/src/polypartition.cpp
34 35
35 36 HEADERS += mainwindow.h \
36 37 pcbgraphicview.h \
@@ -39,6 +40,7 HEADERS += mainwindow.h \
39 40 pcbcontext.h \
40 41 pcbvia.h \
41 42 pcbpad.h \
42 pcbzone.h
43 pcbzone.h \
44 polypartition/src/polypartition.h
43 45
44 46 FORMS += mainwindow.ui
Show file before | Show file after | Hide comments
@@ -110,8 +110,8 void PCBGraphicView::drawBackground(QPai
110 110
111 111 // Shadow
112 112 QRectF sceneRect = this->sceneRect();
113 QRectF rightShadow(sceneRect.right(), sceneRect.top() + 20, 20, sceneRect.height());
114 QRectF bottomShadow(sceneRect.left() + 20, sceneRect.bottom(), sceneRect.width(), 20);
113 QRectF rightShadow(sceneRect.right(), sceneRect.top() + 2, 2, sceneRect.height());
114 QRectF bottomShadow(sceneRect.left() + 2, sceneRect.bottom(), sceneRect.width(), 2);
115 115 if (rightShadow.intersects(rect) || rightShadow.contains(rect))
116 116 painter->fillRect(rightShadow, Qt::darkGray);
117 117 if (bottomShadow.intersects(rect) || bottomShadow.contains(rect))
Show file before | Show file after | Hide comments
@@ -60,8 +60,10 void PCBPad::init( QPointF offset)
60 60 this->addToGroup(rect);
61 61 }
62 62 QGraphicsTextItem* text=new QGraphicsTextItem(QString::number(padNode->padNumber()));
63 text->setScale(0.01);
63 64 text->setPos(rec.center());
64 text->setScale(0.01);
65 // text->setTransformOriginPoint(rec.center());
66 // text->setRotation(padNode->angle());
65 67 text->setZValue(1);
66 68 this->addToGroup(text);
67 69
Show file before | Show file after | Hide comments
@@ -22,41 +22,119
22 22 #include "pcbzone.h"
23 23 #include <QPen>
24 24 #include <QPixmapCache>
25 #include "polypartition/src/polypartition.h"
26
25 27
26 28 PCBZone::PCBZone(QIlib::QIcadPcbZone *zoneNode, PCBContext *context)
27 29 :QGraphicsItemGroup(),zoneNode(zoneNode),context(context)
28 30 {
29 this->init();
31 this->initQtClipping();
30 32 }
31 33
32 void PCBZone::init()
34 void PCBZone::initTriangPolypartition()
35 {
36 TPPLPartition pp;
37 this->setFlags(ItemIsMovable|ItemIsSelectable|ItemIsFocusable);
38 TPPLPoly test;
39 std::list<TPPLPoly> triangles;
40 test.Init(this->zoneNode->filledPolygon.points.points.count());
41 for(int i=0;i<this->zoneNode->filledPolygon.points.points.count();i++)
42 {
43 test[i].x =this->zoneNode->filledPolygon.points.points.at(i)->pos().x();
44 test[i].y =this->zoneNode->filledPolygon.points.points.at(i)->pos().y();
45 }
46 pp.Triangulate_OPT(&test,&triangles);
47 for(std::list<TPPLPoly>::iterator iter = triangles.begin();iter != triangles.end(); iter++)
48 {
49 QPolygonF poly;
50 TPPLPoly t = *iter;
51 for(int i=0;i<t.GetNumPoints();i++)
52 {
53 poly.append(QPointF(t[i].x,t[i].y));
54 }
55 QGraphicsPolygonItem* triangleItem = new QGraphicsPolygonItem();
56 QPen pen = triangleItem->pen();
57 pen.setWidthF(0.05);
58
59 triangleItem->setPen(pen);
60 QBrush brush = triangleItem->brush();
61 brush.setStyle(Qt::SolidPattern);
62 brush.setColor(context->layerColor(this->zoneNode->layer.value()));
63 triangleItem->setBrush(brush);
64 triangleItem->setZValue(-context->layer(this->zoneNode->layer.value()));
65 triangleItem->setPolygon(poly);
66 triangleItem->setCacheMode(QGraphicsItem::DeviceCoordinateCache);
67
68 this->addToGroup(triangleItem);
69 }
70
71 this->setCacheMode(QGraphicsItem::DeviceCoordinateCache);
72 setOpacity(0.6);
73 }
74
75 void PCBZone::initQtClipping()
33 76 {
34 77 this->setFlags(ItemIsMovable|ItemIsSelectable|ItemIsFocusable);
35 78 QPolygonF poly;
36 79 for(int i=0;i<this->zoneNode->filledPolygon.points.points.count();i++)
37 80 {
38 poly.append(this->zoneNode->filledPolygon.points.points.at(i)->pos());
81 QPointF p;
82 p.setX(this->zoneNode->filledPolygon.points.points.at(i)->pos().x());
83 p.setY(this->zoneNode->filledPolygon.points.points.at(i)->pos().y());
84 poly.append(p);
39 85 }
40 QGraphicsPixmapItem* test=new QGraphicsPixmapItem();
41 QPixmap pix;
42 QPainter painter;
43 QGraphicsPolygonItem* polygonItem = new QGraphicsPolygonItem();
44 QPen pen = polygonItem->pen();
45 pen.setWidthF(0.01);
86 QList<QPolygonF> clippedPolygons = splitPolygons(poly,100);
87 for(int i=0;i<clippedPolygons.count();i++)
88 {
89 QGraphicsPolygonItem* polygonItem = new QGraphicsPolygonItem();
90 // QPen pen = polygonItem->pen();
91 // pen.setWidthF(0.01);
46 92
47 polygonItem->setPen(pen);
48 QBrush brush = polygonItem->brush();
49 brush.setStyle(Qt::SolidPattern);
50 brush.setColor(context->layerColor(this->zoneNode->layer.value()));
51 polygonItem->setBrush(brush);
52 polygonItem->setZValue(-context->layer(this->zoneNode->layer.value()));
53 polygonItem->setPolygon(poly);
54 polygonItem->setCacheMode(QGraphicsItem::DeviceCoordinateCache);
55 // test->setPixmap(polygonItem->);
56 //voir doc/qt/...
57 // polygonItem->paint();
58 this->addToGroup(polygonItem);
93 polygonItem->setPen(Qt::NoPen);
94 // polygonItem->setPen(pen);
95 QBrush brush = polygonItem->brush();
96 brush.setStyle(Qt::SolidPattern);
97 brush.setColor(context->layerColor(this->zoneNode->layer.value()));
98 polygonItem->setBrush(brush);
99 polygonItem->setZValue(-context->layer(this->zoneNode->layer.value()));
100 polygonItem->setPolygon(clippedPolygons.at(i));
101 // polygonItem->setCacheMode(QGraphicsItem::DeviceCoordinateCache);
102
103 this->addToGroup(polygonItem);
104 }
105
59 106
60 107 this->setCacheMode(QGraphicsItem::DeviceCoordinateCache);
61 108 setOpacity(0.6);
62 109 }
110
111 QPolygonF intersect(QPointF topLeft,QPointF bottomRight,QPolygonF poly)
112 {
113 QPolygonF rect;
114 rect.append(topLeft);
115 rect.append(QPointF(bottomRight.x(),topLeft.y()));
116 rect.append(bottomRight);
117 rect.append(QPointF(topLeft.x(),bottomRight.y()));
118 return poly.intersected(rect);
119 }
120
121 QList<QPolygonF> PCBZone::splitPolygons(QPolygonF polygon, int maxPoints)
122 {
123 QList<QPolygonF> result;
124 if(polygon.size()>maxPoints)
125 {
126 QRectF brect = polygon.boundingRect();
127 QPointF center = brect.center();
128 QPointF centerLeft = QPointF(brect.x(),brect.center().y());
129 QPointF centerRight = QPointF(brect.topRight().x(),brect.center().y());
130 QPointF topCenter = QPointF(center.x(),brect.topLeft().y());
131 QPointF bottomCenter = QPointF(center.x(),brect.bottomLeft().y());
132 result.append(splitPolygons(intersect(brect.topLeft(),center,polygon),maxPoints));
133 result.append(splitPolygons(intersect(topCenter,centerRight,polygon),maxPoints));
134 result.append(splitPolygons(intersect(center,brect.bottomRight(),polygon),maxPoints));
135 result.append(splitPolygons(intersect(centerLeft,bottomCenter,polygon),maxPoints));
136 }
137 else
138 result.append(polygon);
139 return result;
140 }
Show file before | Show file after | Hide comments
@@ -34,7 +34,9 class PCBZone: public QGraphicsItemGroup
34 34 public:
35 35 PCBZone(QIlib::QIcadPcbZone* zoneNode,PCBContext* context);
36 36 private:
37 void init();
37 void initTriangPolypartition();
38 void initQtClipping();
39 QList<QPolygonF> splitPolygons(QPolygonF polygon,int maxPoints);
38 40 QIlib::QIcadPcbZone* zoneNode;
39 41 int layer;
40 42 PCBContext* context;
General Comments 0
You need to be logged in to leave comments. Login now